Cho tam giác ABC vuông tại A ,đường cao AH .từ H kẻ HE vuông góc AB,HF vuông góc AC A biết HB =4 HC=9 tính EF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GH
22 tháng 6 2023
a) \(BC=BH+HC=3,6+6,4=10\left(cm\right)\)
Tam giác ABC vuông tại A, đường cao AH có:
\(AB^2=BC.BH\\ \Rightarrow AB=\sqrt{BC.BH}=\sqrt{10.3,6}=6\left(cm\right)\)
Tương tự:
\(AC=\sqrt{BC.CH}=\sqrt{10.6,4}=8\left(cm\right)\)
Ta có: \(AH^2=BH.CH\)
\(\Rightarrow AH=\sqrt{BH.CH}=\sqrt{3,6.6,4}=4,8\left(cm\right)\)
b) Tứ giác AEHF là hình chữ nhật (tứ giác có 3 góc vuông) nên EF = AH = 4,8 (cm)
c) Tam giác AHB vuông tại H có EH là đường cao (gt) \(\Rightarrow AH^2=AB.AE\)
Tương tự tam giác AHC ta có \(AH^2=AC.AF\Rightarrow AB.AE=AC.AF\)
Xét tam giác AEF và tam giác ABC có:
\(\widehat{FAE}.chung\)
\(\dfrac{AF}{AB}=\dfrac{AE}{AC}\left(vì.AB.AE=AC.AF\right)\)
Do đó tam giác AEF đồng dạng tam giác ABC.
14 tháng 6 2016
a, áp dụng hệ thức lượng trong tam giác : AC^2 = HC.BC => AC = căn ( HC.BC) = 8 (cm )
AB^2 = HB.BC => AB = căn( HB.BC) = 6 ( cm )
AH.BC = AB.AC => AH = AB.AC : BC =4,8(cm)
b, Trong tam giác vuông HAB, đường cao HE ta có : HA^2 = AB.AE (1)
Trong tam giác vuông HAC, đường cao HF ta có : HA^2 = AC.AF (2)
Từ (1) và (2) ta có : AB.AE = AC.AF ( = AH^2) ( đpcm)
Hình em tự vẽ nhé
25 tháng 4 2018
a) Xét tam giác AHB và tam giác AHC;có:
AH: cạnh chung
AB=AC ( tam giác ABC cân tại A )
góc AHB = góc AHC ( =90 độ )
-> tam giác AHB = tam giác AHC ( ch-gn )
-> HB = HC ( 2 cạnh tương ứng )
b) Ta có: HB = HC ( tam giác AHB = tam giác AHC )
-> HB = HC = BC/2 = 16/2 =8
Ta lại có: tam giác AHB vuông tại H
-> AB2 = AH2+HB2
-> 102 = AH2+82
-> AH2 = 102 - 82
-> AH2 = 100 - 64
-> AH2 = 36
-> AH = 6
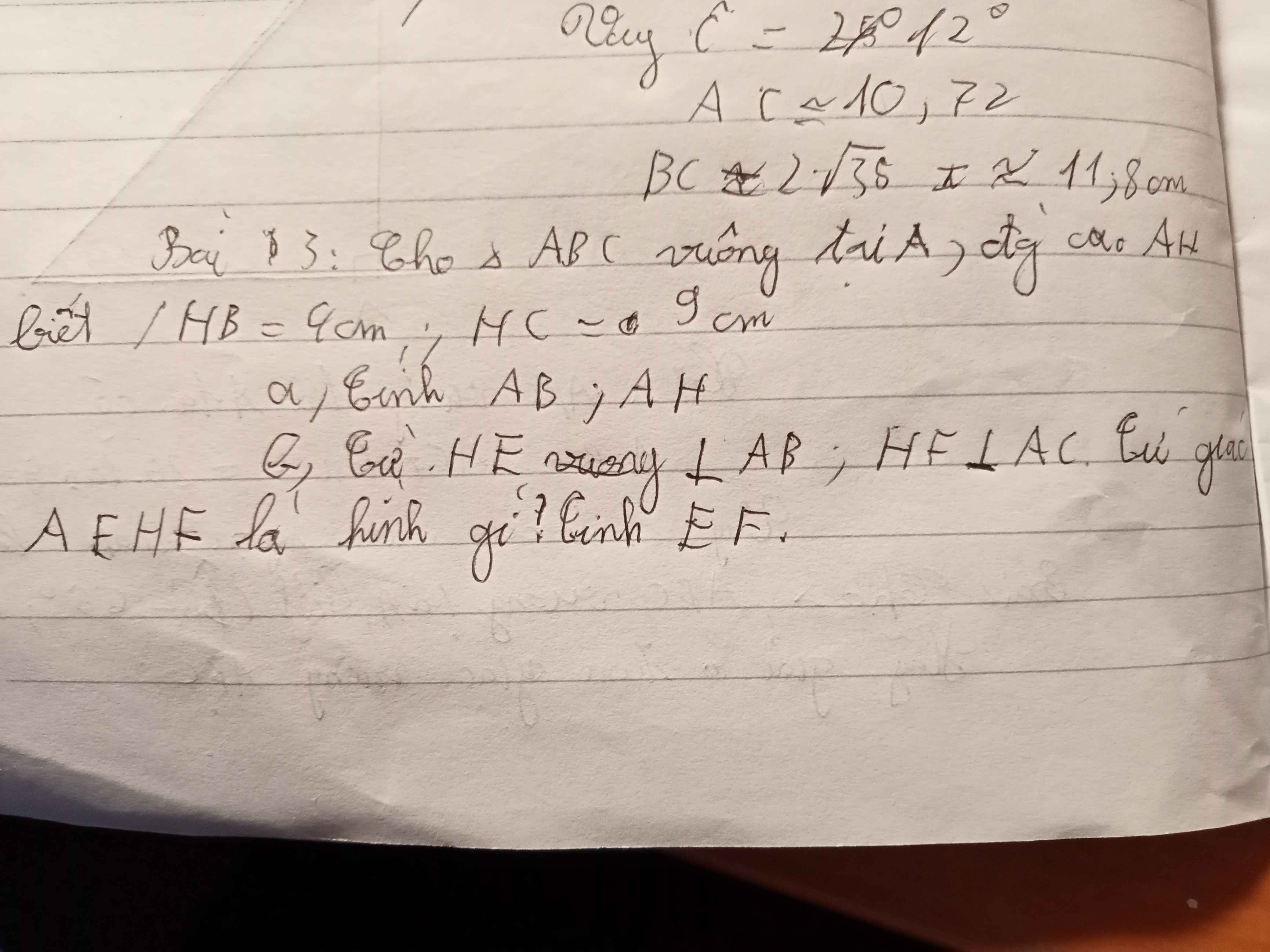
ABC vuông tại A có AH là đường cao
⇒AH² = HB . HC
= 4 . 9
= 36
⇒ AH = 6
Tứ giác AEHF có:
∠HEA = ∠FAE = ∠AFH = 90⁰
⇒ AEHF là hình chữ nhật
⇒ EF = AH = 6