Tính sin2150 + sin2300+ sin2400 + sin2750+ sin2600+ sin2500
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C.
Hai góc 150 và 750 phụ nhau nên sin750 = cos150
Hai góc 200 và 1100 hơn kém nhau 900 nên cos1100 = -sin200
Do đó, A = sin2150 + cos2200 + sin2750 + cos21100
= sin2150 + cos2200 + cos2150 + (-sin200)2 = 2

Chọn B.
Ta có: A= ( sin230 + sin2870) + ( sin2750 + sin2150)
A= (sin230 + cos230) + ( sin2150 + cos2150)
= 1 + 1 = 2

A = sin 2 15 0 + sin 2 25 0 + sin 2 35 0 + sin 2 45 0 + sin 2 55 0 + sin 2 65 0 + sin 2 75 0
Ta có:
A = sin 2 15 0 + sin 2 25 0 + sin 2 35 0 + sin 2 45 0 + sin 2 55 0 + sin 2 65 0 + sin 2 75 0
= sin 2 15 0 + sin 2 25 0 + sin 2 35 0 + sin 2 45 0 + cos 2 35 0 + cos 2 25 0 + cos 2 15 0
= ( sin 2 15 0 + cos 2 15 0 ) + ( sin 2 25 0 + cos 2 25 0 ) + ( sin 2 35 0 + cos 2 35 0 ) + sin 2 45 0
= 1 + 1 + 1 + 2 2 2 = 3 + 1 2 = 7 2
Đáp án cần chọn là: B

d)
sin 2 20 0 + cos 2 30 0 - sin 2 40 0 - sin 2 50 0 + cos 2 60 0 + sin 2 70 0
= sin 2 20 0 + cos 2 30 0 - sin 2 40 0 - c o s 2 40 0 + sin 2 30 0 + cos 2 20 0
= sin 2 20 0 + cos 2 20 0 + cos 2 30 0 + sin 2 30 0 - sin 2 40 0 + cos 2 40 0= 1 + 1 - 1
= 1

Chọn C.
Ta có nhận xét sau:
100 + 800 = 200 + 700 = 300 + 600 = 400 + 500 = 900
nên các cung lượng giác tương ứng đôi một phụ nhau.
Do các góc phụ nhau thì sin góc này bằng cosin góc kia nên ta có:
P = (sin2100 + sin2800) + ( sin2200 + sin2700) + ...+ ( sin2400 + sin2500)
= (sin2100 + cos2100) + ( sin2200 + cos2200) + ...+ ( sin2400 + cos2400)
= 1 + 1 + 1 + 1= 4

2. Tính (+5) + ( +4) = 9
3.Tính (- 9) + ( - 1) = -10
4.Tính : 28 + (-15) = 13
5.Tính (-15) + 12 = - 3
6.Tính (-25) + 25 = 0
7.Tính : 13 - 17 = - 4
8.Tính : (-78) - 9 = - 87
9.Tính : ( -24) - ( - 16) = - 8
10.Tính : 17 - (-3) = 20
11.Tính nhanh : (-21) - ( 48 + 52 - 21) = -100
2, (+5)+(+4)=+9 hoạc 9 cũng được
3, (-9)+(-1)=-10
4, 28+(-15)=13
5, (-15)+12=-3
6, (-25)+25=0
7, 13-17=4
8, (-78)-9=-87
9, (-24)-(-16)=-40
10, 17-(-3)=20
11, (-21+21)-(48-52)=-4
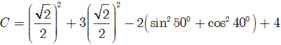
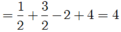
\(=\left(sin^215^0+sin^275^0\right)+\left(sin^230^0+sin^260^0\right)+\left(sin^240^0+sin^250^0\right)\)
\(=\left(sin^215^0+cos^215^0\right)+\left(sin^230^0+cos^230^0\right)+\left(sin^240^0+cos^240^0\right)\)
=1+1+1
=3
\(sin^215^o+sin^230^o+sin^240^o+sin^275^o+sin^260^o+sin^250^o\\ =\left(sin^215^o+sin^275^o\right)+\left(sin^230^o+sin^260^o\right)+\left(sin^240^o+sin^250^o\right)\\ =1+1+1=3\)