Question

[Phượng Phạm]

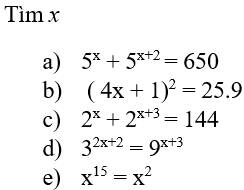
ccau ơi, giúp tớ vs, nhanh nha, chi tiết nx

Answer 1

[@DanHee]

\(a,5^x+5^{x+2}=650\\ \Rightarrow5^x+5^x.5^2=650\\ \Rightarrow5^x\left(1+5^2\right)=650\\ \Rightarrow5^x.26=650\\ \Rightarrow5^x=25\\ \Rightarrow5^x=5^2\\ \Rightarrow x=2\)

\(b,\left(4x+1\right)^2=25.9\\\Rightarrow\left(4x+1\right)^2=225\\ \Rightarrow\left[{}\begin{matrix}4x+1=15\\4x+1=-15\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-4\end{matrix}\right.\)

\(c,2^x+2^{x+3}=144\\ \Rightarrow2^x+2^x.2^3=144\\ \Rightarrow2^x\left(1+2^3\right)=144\\ \Rightarrow2^x=144:\left(1+2^3\right)\\ \Rightarrow2^x=16\\ \Rightarrow2^x=2^4\\ \Rightarrow x=4\)

\(d,3^{x+2}=9^{x+3}\\ \Rightarrow3^{x+2}=\left(3^2\right)^{x+3}\\ \Rightarrow3^{x+2}=3^{2x+6}\\ \Rightarrow x+2=2x+6\\ \Rightarrow x-2x=6-2\\ \Rightarrow-x=4\\ \Rightarrow x=-4\)

\(e,x^{15}=x^2\\ \Rightarrow x^{15}-x^2=0\\ \Rightarrow x^2\left(x^{13}-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x^2=0\\x^{13}-1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)

Answer 2

[Nguyễn Lê Phước Thịnh]

a: =>5^x+5^x*25=650

=>5^x*26=650

=>5^x=25

=>x=2

b: =>4x+1=15 hoặc 4x+1=-15

=>4x=-16 hoặc 4x=14

=>x=7/2 hoặc x=-8

c: =>2^x*9=144

=>2^x=16

=>x=4

d: =>2x+2=2x+6

=>2=6(loại)

e: =>x^2(x^13-1)=0

=>x=0 hoặc x=1