tính tích 2 đơn thức
\(-0,5x^2yz\) và \(-3xy^3z\)
Tìm hệ số và bậc của tích vừa tìm được
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 4 2017
a) Tích của 14xy314xy3 và −2x2yz2−2x2yz2 là:
14xy3.(−2x2yz2)=−12x3y4z214xy3.(−2x2yz2)=−12x3y4z2
Đơn thức tích có hệ số là −12−12 ; có bậc 9.
b) Tích của −2x2yz−2x2yz và −3xy3z−3xy3z là:
−2x2yz.(−3xy3z)=6x3y4z2−2x2yz.(−3xy3z)=6x3y4z2
Đơn thức có hệ số là 6; có bậc 9.
DN
22 tháng 4 2017
a) \(\dfrac{1}{4}xy^3.\left(-2\right)x^2yz^2\)
= \(\left[\dfrac{1}{4}.\left(-2\right)\right].\left(x.x^2\right).\left(y^3.y\right).z^2\)
= \(\dfrac{-1}{2}x^3y^4z^2\).
Đơn thức trên có hệ số là \(\dfrac{-1}{2}\) và bậc là 9.
b) \(-2x^2yz.\left(-3\right)xy^3z\)
= \(\left[\left(-2\right).\left(-3\right)\right].\left(x^2.x\right).\left(y.y^3\right).\left(z.z\right)\)
= 6x\(^3y^4z^2\).
Đơn thức trên có hệ số là 6 và bậc là 9.
NT
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 5 2023
a, Tích hai đơn thức : -0,5 \(x^2\)\(y\)z và -3\(xy^3z\)
A = -0,5 \(x^2\)yz \(\times\) ( -3\(xy^3\)z)
A = 1,5\(x^3\)y4z2
b, bậc của đa thức là: 3 + 4 + 2 = 9
Hệ số cao nhất là 1,5
TH
Thầy Hùng Olm
Manager
VIP
27 tháng 5 2023
Chương trình Toán 7 mới hiện nay chỉ học đơn thức 1 biến, không còn học đơn thức nhiều biến như cũ nữa
HT
0
VD
11 tháng 3 2022
\(a,5x^2y^3z.\left(-11\right)xyz^4=-55x^3y^4z^5\)
Biến : x3y4z5
Hệ số:-55
Bậc:12
b, \(-6x^4y^4\left(-\dfrac{2}{3}\right)x^5y^3z^2=4x^9y^7z^2\)
Biến : x9y7z2
Hệ số:4
Bậc:18
11 tháng 3 2022
\(a)\left(5x^2y^3z\right).\left(-11xyz^4\right)=-55x^3y^4z^5.\)
- Biến: \(x;y;z.\)
- Hệ số: \(-55.\)
- Bậc: \(5.\)
\(b)\left(-6x^4y^4\right).\left(-\dfrac{2}{3}x^5y^3z^2\right)=4x^9y^7z^2.\)
- Biến: \(x;y;z.\)
- Hệ số: \(4.\)
- Bậc: \(9.\)
27 tháng 4 2020
\(\left(-2x^2y\right)^2=\left(-2\right)^2\cdot\left(x^2\right)^2\cdot\left(y\right)^2==4x^4y^2\)
a) Tích hai đơn thức trên : 4x4y2 . -3xy3 = [ 4 . ( -3 ) ] ( x4x ) ( y2y3 ) = -12x5y5
Bậc của đơn thức = 5 + 5 = 10
Hệ số : -12
Phần biến : x5y5
b) Thay x = -1 và y = 2 vào đơn thức tích ta có :
-12 . ( -1 )5 . 25
= -12 . ( -1 ) . 32
= 12 . 32
= 384
Vậy giá trị của đơn thức tích bằng 384 khi x = -1 ; y = 2
NT
2
PT
1
CM
11 tháng 9 2019
Ta có
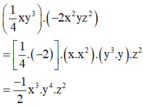
Đơn thức trên có hệ số bằng -1/2.
Bậc của tích trên là tổng bậc của các biến :
Biến x có bậc 3
Biến y có bậc 4
Biến z có bậc 2
⇒ Tích có bậc : 3 + 4 + 2 = 9.
`@` `\text {Ans}`
`\downarrow`
`-0,5x^2yz*(-3xy^3z)`
`= [(-0,5)*(-3)]*(x^2*x)*(y*y^3)*(z*z)`
`= 1,5x^3y^4z^2`
Hệ số: `1,5`
Bậc: `3+4+2 = 9`
`@` `\text {Kaizuu lv u}`
Bạn ơi giải bài tập cho mình với ạ mình cảm ơn nha