Chứng tỏ các đa thức sau không có nghiệm:
a) x8 + 7
b) x2 + 5
c) -x2 - 7
d) x2 + x4 + 7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AD
15 tháng 10 2023
\(C=\left(x^2-1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\\ =\left(x^4-1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\\ =\left(x^8-1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\\ =\left(x^{16}-1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\\ =\left(x^{32}-1\right)\left(x^{32}+1\right)-x^{64}\\ =\left(x^{64}-1\right)-x^{64}\\ =-1\)
Vậy đa thức ko phụ thuộc vào x
T
15 tháng 10 2023
\(C=(x^2-1)(x^2+1)(x^4+1)(x^8+1)(x^{16}+1)(x^{32}+1)-x^{64}\\=(x^4-1)(x^4+1)(x^8+1)(x^{16}+1)(x^{32}+1)-x^{64}\\=(x^8-1)(x^8+1)(x^{16}+1)(x^{32}+1)-x^{64}\\=(x^{16}-1)(x^{16}+1)(x^{32}+1)-x^{64}\\=(x^{32}-1)(x^{32}+1)-x^{64}\\=x^{64}-1-x^{64}\\=-1\)
⇒ Giá trị của C không phụ thuộc vào giá trị của biến
ML
3
18 tháng 5 2021
a) \(x^2+4\)
Ta có: \(x^2\ge0\) với mọi x
=> \(x^2+4\ge4>0\) với mọi x.
=> Pt vô nghiệm
b) \(10x^2+3\)
Ta có: \(x^2\ge0\) với mọi x
=> \(10x^2\ge0\) với mọi x
=> \(10x^2+3\ge3>0\) với mọi x.
=> Pt vô nghiệm.
c) Bài này đề sai nhé.
d) Bài này đề cũng sai nốt:v
10 tháng 4 2023
`a,`
`f(x)=x^2+4x+10`
\(\text{Vì }\)\(x^2\ge0\left(\forall x\right)\)
`->`\(x^2+4x+10\ge10>0\left(\forall\text{ x}\right)\)
`->` Đa thức không có nghiệm (vô nghiệm).
`c,`
`f(x)=5x^4+x^2+` gì nữa bạn nhỉ? Mình đặt vd là 1 đi nha :v.
Vì \(x^4\ge0\text{ }\forall\text{ }x\rightarrow5x^4\ge0\text{ }\forall\text{ }x\)
\(x^2\ge0\text{ }\forall\text{ }x\)
`->`\(5x^4+x^2+1\ge1>0\text{ }\forall\text{ }x\)
`->` Đa thức vô nghiệm.
`b,`
`g(x)=x^2-2x+2017`
Vì \(x^2\ge0\text{ }\forall\text{ }x\)
`->`\(x^2-2x+2017\ge2017\text{ }\forall\text{ }x\)
`->` Đa thức vô nghiệm.
`d,`
`g(x)=4x^2004+x^2018+1`
Vì \(x^{2004}\ge0\text{ }\forall\text{ }x\rightarrow4x^{2004}\ge0\text{ }\forall\text{ }x\)
\(x^{2018}\ge0\text{ }\forall\text{ }x\)
`->`\(4x^{2004}+x^{2018}+1\ge1>0\text{ }\forall\text{ }x\)
`->` Đa thức vô nghiệm.
NN
4
MH
8 tháng 4 2022
Mũ chẵn lớn hơn bằng 0 mà cộng thêm 1 số không âm nữa nên các đa thức trên luôn lớn hơn 0
8 tháng 4 2022
a: Vì \(x^2+1>0\forall x\)
nên đa thức này vô nghiệm
b: \(2x^2+1>0\forall x\)
nên đa thức này vô nghiệm
c: \(x^4+2>0\forall x\)
nên đa thức này vô nghiệm
20 tháng 5 2021
Cho A(x) = 0, có:
x2 - 4x = 0
=> x (x - 4) = 0
=> x = 0 hay x - 4 = 0
=> x = 0 hay x = 4
Vậy: x = 0; x = 4 là nghiệm của đa thức A(x)
PT
1
CM
10 tháng 1 2017
Thay x = -1 và đa thức, ta có:
(-1)2 + (-1)4 + (-1)6 + … + (-1)100 =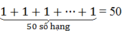 
Vậy giá trị đa thức bằng 50 tại x = -1.
20 tháng 5 2021
x4+x3+x+1 = x3. (x+1) + (x+1) = (x3 + 1)(x+1) = (x+1)2.(x2 - x +1) = 0
=> x + 1 = 0 => x = -1
Vì x2 - x + 1 = (x2 - 2.x .1/2 + 1/4) + 3/4 = (x - 1/2)2 + 3/4 >0 + 3/4 = 3/4
Vậy đa thức trên có nghiệm là x = -1
AH
Akai Haruma
Giáo viên
7 tháng 9 2021
Lời giải:
a.
$x^8+x^4+1=(x^4)^2+2x^4+1-x^4$
$=(x^4+1)^2-(x^2)^2=(x^4+1-x^2)(x^4+1+x^2)$
$=(x^4+1-x^2)[(x^2+1)^2-x^2]$
$=(x^4-x^2+1)(x^2+1-x)(x^2+1+x)$
b.
$x^{12}-3x^6-1=(x^6-\frac{3}{2})^2-\frac{13}{4}$
$=(x^6-\frac{3}{2}-\frac{\sqrt{13}}{2})(x^6-\frac{3}{2}+\frac{\sqrt{13}}{2})$
c.
$3x^4+10x^2-25=(3x^4+15x^2)-(5x^2+25)$
$=3x^2(x^2+5)-5(x^2+5)=(x^2+5)(3x^2-5)$
$=(x^2+5)(\sqrt{3}x-\sqrt{5})(\sqrt{3}x+\sqrt{5})$
c.
$x^2-5y^2-y^4+2xy-9$
$=(x^2+2xy+y^2)-(y^4+6y^2+9)$
$=(x+y)^2-(y^2+3)^2$
$=(x+y+y^2+3)(x+y-y^2-3)$
7 tháng 9 2021
\(a,x^8+x^4+1\\ =\left(x^8+2x^4+1\right)-x^4\\ =\left(x^4+1\right)^2-x^4\\ =\left(x^4-x^2+1\right)\left(x^4+x^2+1\right)\\ b,x^{12}-3x^6-1\\ =\left(x^{12}-2x^6+1\right)-x^6-2\\ =\left(x^6-1\right)^2-x^6-2\\ =\left(x^6-x^3-1\right)\left(x^6+x^3-1\right)-2???\\ c,3x^4+10x^2-25\\ =4x^4-\left(x^4-10x^2+25\right)\\ =4x^4-\left(x^2-5\right)^2\\ =\left(2x^2-x^2+5\right)\left(2x^2+x^2-5\right)\\ =\left(x^2+5\right)\left(3x^2-5\right)\\ d,x^2-5y^2-y^4+2xy-9\\ =\left(x^2+2xy+y^2\right)-\left(y^4+6y^2+9\right)\\ =\left(x+y\right)^2-\left(y^2+3\right)^2\\ =\left(x+y+y^2+3\right)\left(x+y-y^2-3\right)\)
21 tháng 5 2021
`M(x)=P(x)+Q(x)`
`=x^4-5x+2x^2+1+5x+x^2+5-3x^2+x^4`
`=2x^4+6`
Đặt `M(x)=0`
`<=>2x^4+6=0`
`<=>x^4=-3`(vô lý vì `x^4>=0`)
22 tháng 5 2021
a) Ta có M(x)=P(x)+Q(x)
=(\(x^4-5x+2x^2+1\))+(\(5x+x^2+5-3x^2+x^4\))
=\(x^4-5x+2x^2+1\)+\(5x+x^2+5-3x^2+x^4\)
=(\(x^4+x^4\))+(-5x+5x)+(\(2x^2\)+\(x^2\)-\(3x^2\))+(1+5)
=\(2x^4\)+6
Vậy M(x)=\(2x^4+6\)
b)Vì 2x\(^4\)\(\ge\) 0 với \(\forall\) x
nên \(2x^4+6\) \(\ge\)0 với \(\forall\)x
\(\Rightarrow\)M(x) \(\ge\) 0 với \(\forall\) x
Vậy M(x) vô nghiệm
a) \(x^8+7=0\) <=> \(x^8=-7\) (vô lí vì x^8 >=0) => pt vô nghiệm
b)\(x^2+5=0\) <= > \(x^2=-5\)(vô lí vì x^2 >=0) => pt vô nghiệm
c)\(-x^2-7=0\)<=> \(-x^2=7\)<=>\(x^2=-7\)(vô lí vì x^2 >=0) => pt vô nghiệm
d)\(x^2+x^4+7=0\)<=>\(x^2+x^4=-7\)(vô lí vì x^2 >=0, x^4 >=0) => pt vô nghiệm
a) do x^8 lớn hơn hoặc = 0 vs mọi x => x^8 + 7 > 0 => x^8 + 7 vô nghiệm
b) làm như câu a
c) cái này mik ko bik làm
d) Do x^2; x^4 lớn hơn hoặc = 0 vs mọi x => x^2 + x^4 + 7 > 0 => x^2 + x^4 + 7 vô nghiệm