cho tam giác ABC cân tại A. gọi I là giao điểm thuộc cạnh BC sao cho BI=BA và H là trung diểm cuả AI.tia BH cắt AC tại E. tia IE cắt tia BA tại M. cm rằng
a)tam giác ABH= am giác IBH
b)tam giácAEI cân
c) EM lớn hơn EI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 5 2023
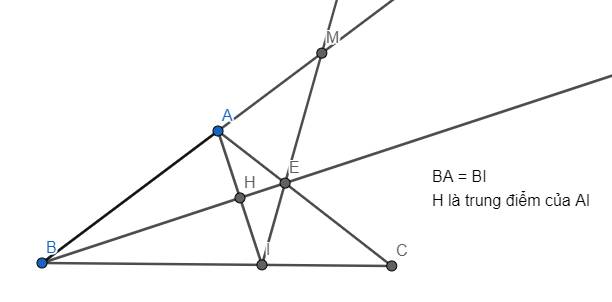
a) Xét ΔABI có:
- BA = BI, suy ra ΔABI cân tại B
- BH là đường trung tuyến đáy AI của ΔABI (do H là trung điểm của AI)
Suy ra BH cũng là đường cao, cũng là đường trung trực của ΔABI.
Khi đó ΔABH & ΔIBH đều vuông tại H. Hai tam giác này có BH là cạnh chung và BA = BI (giả thuyết) nên ΔABH = ΔIBH (cạnh huyền - cạnh góc vuông).
b) Vì BH là đường trung trực của ΔABI (chứng minh trên) và E thuộc BH nên EA = EI. Suy ra ΔAEI cân.
6 tháng 9 2023
a: Xét ΔBAI và ΔBDI có
BA=BD
AI=DI
BI chung
=>ΔBAI=ΔBDI
b:
ΔBAI=ΔBDI
=>góc ABI=góc DBI
=>góc ABE=góc DBE
Xét ΔBAE và ΔBDE có
BE chung
góc ABE=góc DBE
BA=BD
Do đó; ΔBAE=ΔBDE
=>EA=ED và góc BDE=góc BAE
=>ΔEAD cân tại E và góc BDE=90 độ
c: EA=ED
EA<EF
Do đó: ED<EF
20 tháng 3 2023
a: ΔBAD cân tại B
mà BH là trung tuyến
nên BH vuông góc AD
Xet ΔEAD có
EH vừa là đường cao, vừa là trung tuyến
=>ΔEAD cân tại E
b: EA=ED
mà EA<EM
nên ED<EM
23 tháng 3 2023
a: ΔBAD cân tại B
mà BH là trung tuyến
nên BH là phân giác của góc ABD
Xét ΔBAE và ΔBDE có
BA=BD
góc ABE=góc DBE
BE chung
=>ΔBAE=ΔBDE
=>EA=ED
b: EA=ED
mà EA<EM
nên ED<EM
23 tháng 3 2023
a: ΔBAD cân tại B
mà BH là trung tuyến
nên BH là phân giác của góc ABD
Xét ΔBAE và ΔBDE có
BA=BD
góc ABE=góc DBE
BE chung
=>ΔBAE=ΔBDE
=>EA=ED
b: EA=ED
mà EA<EM
nên ED<EM