Cho hình vuông ABCD có diện tích là 16 cm vuông kéo dài AB về phía B một đoạn BM dài 2 cm nối M với C rồi kéo dài các AD kéo dài tại N tính đoạn ND
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 4 2015
125,125 + 175,175 + 214,214 + 172,172 + 219,219
= Lấy máy tính mà tính có gì nhắn tin cho mình nha
12 tháng 10 2016
Sơ đồ minh họa:
Theo đề bài toán thì \(CP=4cm\). Vẽ hình vuông \(CPKE\). Khi đó \(DE\) bằng độ dài chiều rộng hình chữ nhật \(ABCD\).
Trên cạnh \(DQ\) lấy điểm \(H\) sao cho \(DH=HQ=2cm\). Vẽ hình chữ nhật \(DEGH\) ( \(G\) nằm trên \(EK\) ). Khi đó diện tích hình chữ nhật \(BMNC\) bằng diện tích hình chữ nhật \(DEGH\).
Do đó diện tích hình vuông \(ABPQ\) hơn diện tích hình chữ nhật \(AMND\) chính là diện tích phần tô đậm ( bằng tổng diện tích hình vuông \(CPKE\) và diện tích hình chữ nhật \(HGKQ\) ).
Diện tích hình vuông \(CPKE\) là:
\(4\times4=16\left(cm^2\right)\)
Diện tích hình chữ nhật \(HGKQ\) là:
\(22-16=6\left(cm^2\right)\)
Độ dài cạnh \(HG\) là:
\(6\div2=3\left(cm\right)\)
Cạnh hình vuông \(ABPQ\) là:
\(3+4=7\left(cm\right)\)
Diện tích hình vuông \(ABPQ\) là:
\(7\times7=49\left(cm^2\right)\)
20 tháng 6 2017
Chiều cao của tam giác ANM là :
12 + 3 = 15 ( cm )
Độ dài đáy AM là :
9 + 3 = 12 ( cm )
Diện tích tam giác AMN là :
\(\frac{1}{2}\)x 15 x 12 = 90 ( cm\(^2\))
Đáp số : 90 cm\(^2\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
10 tháng 9 2020
Nối M với C; N với D; P với A và Q với B
Nối A với C; B với D
Ta có S(ABCD)=S(ABD)+S(BCD)=S(ABC)+S(ACD)
Xét tg ABQ và tg ABD có chung đường cao hạ từ B xuống DQ và cạnh đáy AQ=AD nên S(ABQ)=S(ABD)
Xét tg ABQ và tg BMQ có chung đường cao hạ từ Q xuống AM và cạnh đáy AB=BM nên S(ABQ)=S(BMQ)
=> S(ABQ)=S(BMQ)=S(ABD) => S(AMQ)=S(ABQ)+S(BMQ)=2xS(ABD) (1)
Chứng minh tương tự khi xét các tam giác BCD với tg CDN và tg CDN với tg DNQ => S(CNP)=2xS(BCD) (2)
Từ (1) và (2) => S(AMQ)+S(CNP)=2xS(ABD)+2xS(BCD)=2x[S(ABD)+S(BCD)]=2xS(ABCD)
Chứng minh tương tự ta sẽ có kết quả S(DPQ)+S(CMN)=2x[S(ACD)+S(ABC)]=2xS(ABCD)
S(MNPQ)=[S(AMQ)+S(CNP)]+[S(DPQ)+S(CMN)]+S(ABCD)=5xS(ABCD)=5x25=125 cm2
3 tháng 4 2023
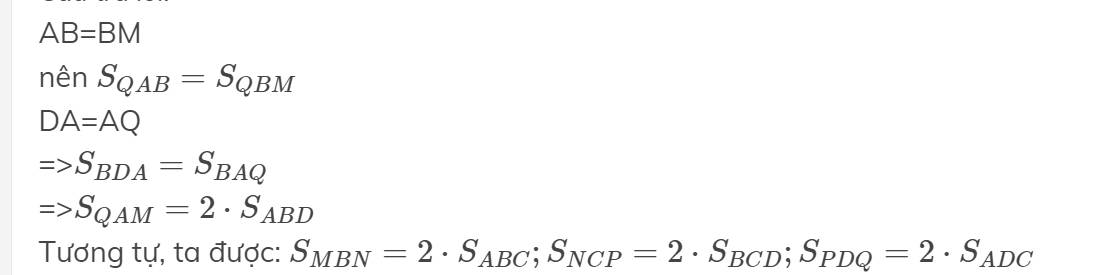
=>\(S_{MNPQ}=S_{MBN}+S_{NCP}+S_{PDQ}+S_{QMA}+S_{ABCD}\)
\(=5\cdot S_{ABCD}=5\cdot25=125\left(cm^2\right)\)
