cách chứng minh đường thẳng là trung trực của đoạn thẳng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MN
2
27 tháng 6 2016
* Chứng minh bằng tiếng việt:
Kẻ tam giác ABC; H,I,K lần lượt là trung điểm AC,BC,AB. Kẻ các đường thẳng vuông góc AC,BC giao nhau tại O, kẻ đường trung trực của AB.
B1: Chứng minh OH và OI đồng quy (phương pháp phản chứng):
Giả sử OH song song OI.
Mà OH vuông góc AC, OI vuông góc BC => AC song song BC => Vô lí
=> OH và OI đồng quy tại O.
B2: Chứng minh 3 đường trung trực đồng quy.
Áp dụng tính chất về đường trung trực của đoạn thẳng: Tất cả các điểm nằm trên đường trung trực của đoạn thẳng đều cách đều 2 đầu mút của đoạn thẳng.
Vậy áp dụng tính chất trên, ta suy ra OA=OB và OA=OC
=> OB=OC
Áp dụng tính chất: nếu một điểm cách đều 2 đầu mút đoạn thẳng thì điểm đó nằm trên đường trung trực của đoạn đó
=> O nằm trên đường trung trực của AB
Vậy => ĐPCM
27 tháng 6 2016
Bài này trong giáo dục việt nam không có nên mình đoán là bạn học thêm hoặc là học tiếng pháp
DT
27 tháng 4 2019
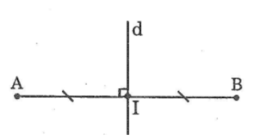
1. vd: đường thẳng d là đường trung trực của đoạn thẳng AB
- ta c/m đường thẳng d vuông góc vs đoạn thẳng AB tại trung điểm của AB
2. ta tìm giao của 2 đg thẳng sau đó c/m đg thẳng thứ 3 cx đi qua giao điểm đó
sử dụng các t/c đồng quy trong t.giác(sgk 7 tập 2)
6 tháng 1 2022
a: Ta có: M nằm trên đường trung trực của AB
nên MA=MB
b: Ta có: ΔMAB cân tại M
mà MI là đường trung trực
nên MI là đường phân giác
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
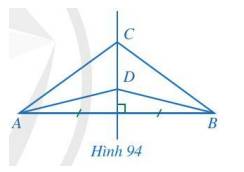
Ta có: đường thẳng CD là đường trung trực của đoạn thẳng AB nên CA=CB và DA=DB.
Ta có tam giác ABC cân tại C, tam giác DAB cân tại D
Suy ra \(\widehat {CAB} = \widehat {CBA};\widehat {DAB} = \widehat {DBA}\).
Vậy \(\widehat {CAB} - \widehat {DAB} = \widehat {CBA} - \widehat {DBA}\) suy ra: \(\widehat {CAD} = \widehat {CBD}\).
CM
17 tháng 2 2017
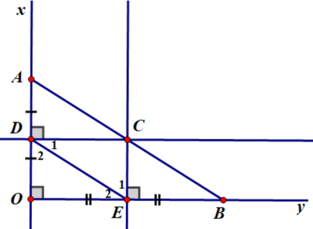
Chứng minh tương tự như d suy ra CB // DE.
Do đó theo tiên đề Ơ-clit ta suy ra hai đường thẳng BC và CA trùng nhau hay A, B, C thẳng hàng.
CM
6 tháng 8 2017
- Vẽ đoạn thẳng AB = 24mm
- Vẽ trung điểm I cuả AB
Vì I là trung điểm của AB nên IA = IB = AB/2 = 12 (mm)
Đặt thước thẳng trùng với đường thẳng AB sao cho vạch 0 trùng với điểm A , vạch 12 cho ta vị trí điểm I.
- Vẽ đường thẳng d đi qua I và d⊥ AB
Đặt êke sao cho một cạnh góc vuông của êke trùng với đường thẳng AB, đỉnh góc vuông của êke trùng với I, vẽ đường thẳng đi qua cạnh góc vuông còn lại của êke ta được đường thẳng d.
Khi đó d là trung trực của AB.
17 tháng 1 2022
b: Gọi O là điểm nằm trên đường trung trực của AB
=>OH⊥AB tại H
=>H là trung điểm của AB
Xét ΔOHA vuông tại H và ΔOHB vuông tại H có
OH chung
HA=HB
Do đó: ΔOHA=ΔOHB
Suy ra: OA=OB
Ta có PM = PN ( bán kính đường tròn)
nên P ? đường trung trực của MN
QM = QN ( bán kính đường tròn)
? Q ? đường trung trực của MN
Vậy PQ là đường trung trực của đoạn
thẳng MN