Tìm m để hàm số y=x2-4x+m+5 có GTNN trên đoạn[3,7] bằng 10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
\(c,\text{PT có 2 }n_0\text{ phân biệt }\Leftrightarrow\Delta'=2^2-2m>0\Leftrightarrow2m< 4\Leftrightarrow m< 2\)

Đáp án C
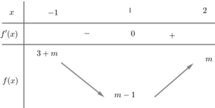
Xét hàm số f x = x 2 − 2 x + m trên đoạn [-1;2]
Tạ có: f ' x = 2 x − 2 = 0 ⇒ x = 1
Lại có: f 0 = m ; f − 1 = m − 1 ; f 2 = m + 2
Do đó f x ∈ m − 1 ; m + 2
Nếu m − 1 ≥ 0 ⇒ max 0 ; 2 f x = m + 2 = 5 ⇔ m = 3
Nếu m − 1 < 0 suy ra max 0 ; 2 f x = m + 2 max 0 ; 2 f x = 1 − m
TH1: max 0 ; 2 f x = m + 2 = 5 ⇔ m = 3 k o _ t / m
TH2: max 0 ; 2 f x = 1 − m ⇔ m = − 4 ⇒ m + 1 = − 3 t / m
Vậy m = 3 ; m = − 4 là giá trị cần tìm

a) Để hàm số đạt giá trị nhỏ nhất bằng 0 khi x=0 thì 2m-1>0
\(\Leftrightarrow2m>1\)
hay \(m>\dfrac{1}{2}\)
b) Để hàm số đồng biến khi x<0 và nghịch biến khi x>0 thì 2m-1<0
\(\Leftrightarrow2m< 1\)
hay \(m< \dfrac{1}{2}\)



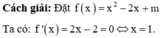

Lời giải:
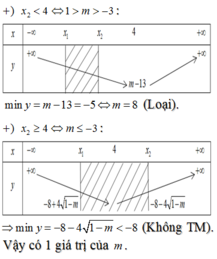
$y=x^2-4x+m+5=x(x-3)-(x-3)+m+2$
$=(x-1)(x-3)+m+2$
Với $x\in [3;7]$ thì $(x-1)(x-3)\geq 0$
$\Rightarrow y\geq m+2$
Vậy $y_{\min}=m+2=10$
$\Leftrightarrow m=8$