

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đạo hàm f'(x) = m 2 - m + 1 ( x + 1 ) 2 > 0, ∀ x ∈ [ 0 ; 1 ]
Suy ra hàm số f(x) đồng biến trên [0; 1] nên min f(x) = f(0) = -m2+m
Theo bài ta có:
-m2+ m= -2 nên m= -1 hoặc m= 2.
Chọn D.

+ Đạo hàm f'(x) = 2 - m x 2 ( x + 1 ) x ( x + 1 )
f'(x) = 0 ⇒ x = 2 m ↔ x = m 2 4 ∈ [ 0 ; 4 ] , ∀ m > 1
+ Lập bảng biến thiên, ta kết luận được
m a x [ 0 ; 4 ] f ( x ) = f ( 4 m 2 ) = m 2 + 4
+ Vậy ta cần có m 2 + 4 < 3
↔ m < 5 → m > 1 m ∈ ( 1 ; 5 )
Chọn C.

+ Xét hàm số f(x) =x2- 2x trên đoạn [ -1; 2],
+ ta có đạo hàm f’(x) = 2( x-1) và f’( x) =0 khi x= 1
Vậy:
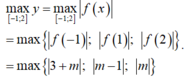
TH1: Với m a x [ - 1 , 2 ] = | m - 1 | ,
ta có m - 1 ≥ m + 3 | m - 1 | ≥ | m | | m - 1 | = 5
↔ | m - 1 | ≥ m + 3 | m - 1 | ≥ | m | m = - 4 ∨ m = 6 ↔ m = - 4
TH2: Với
m a x [ - 1 , 2 ] y = | m + 3 | ↔ | m + 3 | ≥ | m - 1 | | m + 3 | ≥ | m | | m + 3 | ≥ 5
↔ | m + 3 | ≥ | | m - 1 | | m + 3 | ≥ | m | m = 2 ∨ m = - 8 ↔ m = 2
TH3: Với
m a x [ - 1 , 2 ] y = | m | ↔ | m | ≥ | m - 1 | | m | ≥ | m + 3 | | m | = 5 ↔ | m | ≥ | m - 1 | | m | ≥ | m + 3 | m = 5 ∨ m = - 5
( vô nghiệm)
Chọn D.

Chọn D
Điều kiện: x ≠ m
Hàm số đã cho xác định trên [0;4] khi ![]()
Ta có 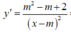
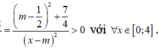
Hàm số đồng biến trên đoạn [0;4] nên 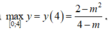
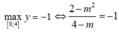
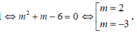
Kết hợp với điều kiện (*) ta được m = -3. Do đó có một giá trị của m thỏa yêu cầu bài toán.