với giá trị nào của a b c thì f(x) = g(x)
f(x) =x^ 3 + 1
g(x) = ( x + a ) (x^2 + bx +c )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LN
1
Những câu hỏi liên quan
11 tháng 12 2021
\(a,\Leftrightarrow f\left(x\right)⋮g\left(x\right)=\left(x+2\right)^2\\ \Leftrightarrow f\left(-2\right)=-8+4a-4=0\\ \Leftrightarrow a=3\\ b,\Leftrightarrow f\left(x\right)⋮g\left(x\right)=\left(x-1\right)\left(x+1\right)\\ \Leftrightarrow f\left(1\right)=f\left(-1\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}1+a+b-1=0\\1-a-b-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=0\\a+b=0\end{matrix}\right.\Leftrightarrow a,b\in R\\ \text{Vậy }f\left(x\right)⋮g\left(x\right),\forall a,b\\ c,\Leftrightarrow f\left(1\right)=f\left(-2\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}2-3a+2+b=0\\-18-12a-4+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a-b=4\\12a-b=-22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{26}{9}\\b=-\dfrac{38}{3}\end{matrix}\right.\)
15 tháng 6 2016
f(x)=x3+1=(x+1)(x2-x+1)
Mà f(x)=g(x)=(x+a)(x2+bx+c)
Nên: a=1;b=-1;c=1
HN
15 tháng 6 2016
ta có : f(x)=x3+1=(x+1)(x2-x+1).
lại có: g(x)=(x+a)(x2+bx+c)
để f(x)=g(x) thì (x+1)(x2-x+1)=(x+a)(x2+bx+c)
<=> \(\begin{cases}x+1=x+a\\x^2-x+1=x^2+bx+c\end{cases}\)
<=>\(\begin{cases}a=1\\b=-1\\c=1\end{cases}\)
vậy với a=1, b=-1 và c=1 thì f(x)=g(x)
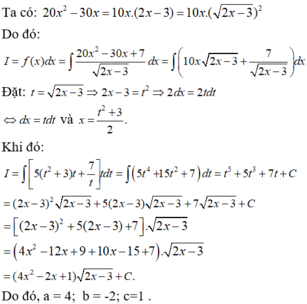
f(x) = g(x)
=>x3+1=(x+a)(x2+bx+c)
<=>(x+1)(x2-1.x+1)
=>a=c=1;b=-1