Khảo sát và vẽ đồ thị hàm số sau:
\(y=\left(\dfrac{5}{2}\right)^{\left|x\right|}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Thay x=1 vào \(y=-\dfrac{5}{2}x\), ta được:
\(y=-\dfrac{5}{2}\cdot1=-\dfrac{5}{2}\)
Vậy: \(A\left(1;-\dfrac{5}{2}\right)\) thuộc đồ thị hàm số y=-5/2x
b: Thay x=2 vào \(y=-\dfrac{5}{2}x\), ta được:
\(y=-\dfrac{5}{2}\cdot2=-5\)
=>B(2;-5) thuộc đồ thị hàm số y=-5/2x
Thay x=3 vào y=-5/2x, ta được:
\(y=-\dfrac{5}{2}\cdot3=-\dfrac{15}{2}\)<>7
=>\(C\left(3;7\right)\) không thuộc đồ thị hàm số y=-5/2x
Thay x=1 vào y=-5/2x, ta được:
\(y=-\dfrac{5}{2}\cdot1=-\dfrac{5}{2}\)<>5/2
=>\(D\left(1;\dfrac{5}{2}\right)\) không thuộc đồ thị hàm số \(y=-\dfrac{5}{2}x\)
Thay x=0 vào \(y=-\dfrac{5}{2}x\), ta được:
\(y=-\dfrac{5}{2}\cdot0=0\)<>4
=>E(0;4) không thuộc đồ thị hàm số \(y=-\dfrac{5}{2}x\)



nên từ đồ thị (C) ta suy ra ngay đồ thị của hàm số :
\(y=\left|\dfrac{x^3}{6}+\dfrac{3x^2}{2}+\dfrac{5x}{2}\right|\) là hình 18


1: Khi m=1 thì (d1): y=x+3 và (d2): y=-x+3
a: 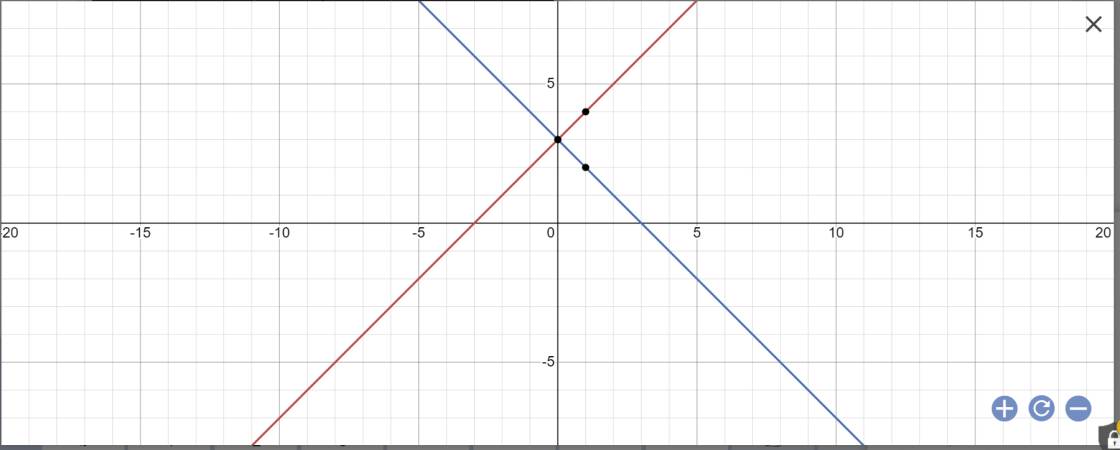
b: Tọa độ giao điểm là:
x+3=-x+3 và y=x+3
=>x=0 và y=3

a) 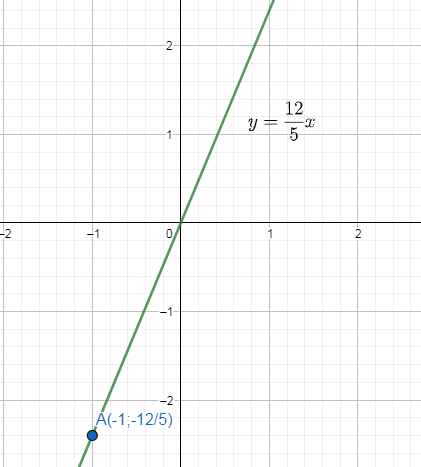
b) Trong các điểm trên, không có điểm nào thuộc đồ thị hàm số.