Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) 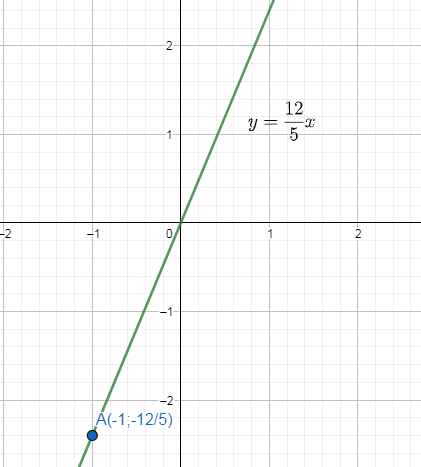
b) Trong các điểm trên, không có điểm nào thuộc đồ thị hàm số.

1: Khi m=1 thì (d1): y=x+3 và (d2): y=-x+3
a: 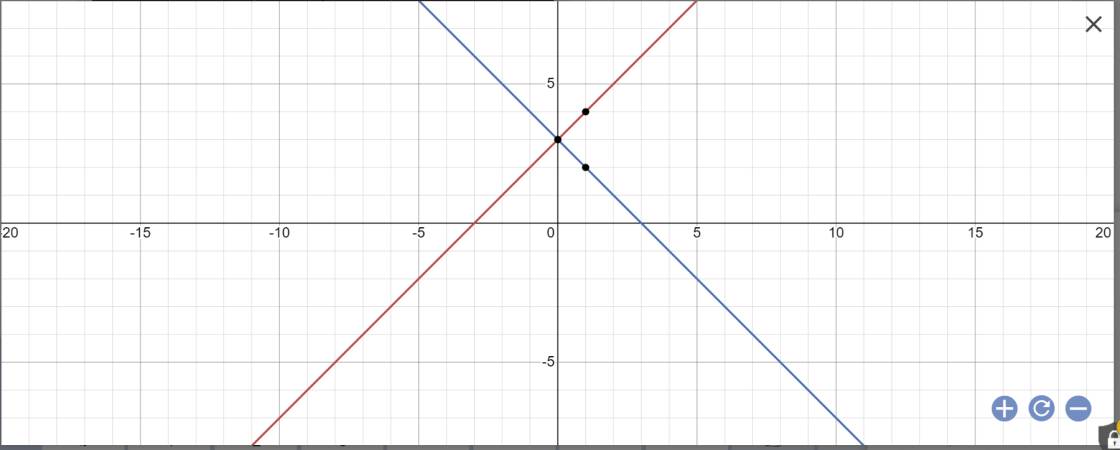
b: Tọa độ giao điểm là:
x+3=-x+3 và y=x+3
=>x=0 và y=3

Bài 1:
a: Thay x=-2 và y=2 vào hàm số, ta được:
4a=2
hay a=1/2
Bài 2:
a: \(\Leftrightarrow\left\{{}\begin{matrix}4x+5y=3\\4x-12y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}17y=-17\\x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\3y=x-5=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)
b: \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}=1\\\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{y}=\dfrac{1}{2}-\dfrac{1}{5}=\dfrac{3}{10}\end{matrix}\right.\Leftrightarrow\left(x,y\right)=\left(2;\dfrac{10}{3}\right)\)

Hàm số \(y=\sqrt{3-m}\left(x+5\right)\) là hàm số bậc nhất khi \(\sqrt{3-m}\ne0\)
\(\Leftrightarrow3-m\ne0\)
\(\Leftrightarrow m\ne3\)
Tọa độ giao điểm của hai đồ thị hàm số \(y=\dfrac{1}{2}x-2\) và \(y=\dfrac{3}{2}x-2\) là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{2}x-2=\dfrac{3}{2}x-2\\y=\dfrac{1}{2}x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{2}x-2-\dfrac{3}{2}x+2=0\\y=\dfrac{1}{2}x-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x=0\\y=\dfrac{1}{2}x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{2}\cdot0-2=-2\end{matrix}\right.\)
Vậy: Hai đồ thị hàm số \(y=\dfrac{1}{2}x-2\) và \(y=\dfrac{3}{2}x-2\) có tọa độ giao điểm là (0;-2)
\(y=\sqrt{3-m}.\left(x+5\right)\) là hàm số bậc nhất \(\Leftrightarrow\sqrt{3-m}\ne0\Leftrightarrow m\ne3\)
Lập PT hoành độ ta có:
\(\dfrac{1}{2}x-2=\dfrac{3}{2}x-2\)
\(\Leftrightarrow x=0\)
\(\Rightarrow y=\dfrac{1}{2}.0-2=-2\)
=> Tọa độ (0;-2)

Câu 2:
c) Phương trình hoành độ giao điểm của (P) và (d) là:
\(\dfrac{1}{2}x^2=2x+6\)
\(\Leftrightarrow\dfrac{1}{2}x^2-2x-6=0\)
\(\Leftrightarrow x^2-4x-12=0\)
\(\Leftrightarrow x^2-4x+4=16\)
\(\Leftrightarrow\left(x-2\right)^2=16\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=4\\x-2=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\)
Thay x=6 vào (P), ta được:
\(y=\dfrac{1}{2}\cdot6^2=18\)
Thay x=-2 vào (P), ta được:
\(y=\dfrac{1}{2}\cdot\left(-2\right)^2=\dfrac{1}{2}\cdot4=2\)
Vậy: Tọa độ giao điểm của (P) và (d) là (6;18) và (-2;2)
Câu 3:
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-2\right)}{1}=2\\x_1\cdot x_2=\dfrac{c}{a}=\dfrac{-1}{1}=-1\end{matrix}\right.\)
Ta có: \(P=x_1^3+x_2^3\)
\(=\left(x_1+x_2\right)^3-3\cdot x_1x_2\left(x_1+x_2\right)\)
\(=2^3-3\cdot\left(-1\right)\cdot2\)
\(=8+3\cdot2\)
\(=8+6=14\)
Vậy: P=14

1: Bạn bổ sung đề bài đi bạn
2: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(2m-1\right)x-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\\left(2m-1\right)x=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{4}{2m-1}\\y=0\end{matrix}\right.\)
=>\(OA=\sqrt{\left(\dfrac{4}{2m-1}-0\right)^2+\left(0-0\right)^2}=\dfrac{4}{\left|2m-1\right|}\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=\left(2m-1\right)x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\left(2m-1\right)\cdot0-4=-4\end{matrix}\right.\)
=>OB=4
Để ΔOAB cân tại O thì OA=OB
=>\(\dfrac{4}{\left|2m-1\right|}=4\)
=>\(\dfrac{1}{\left|2m-1\right|}=1\)
=>\(\left|2m-1\right|=1\)
=>\(\left[{}\begin{matrix}2m-1=1\\2m-1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2m=2\\2m=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1\\m=0\end{matrix}\right.\)

Vì hai đồ thị cắt nhau tại một điểm trên trục tung nên n=-4
=>m=-2
a: Thay x=1 vào \(y=-\dfrac{5}{2}x\), ta được:
\(y=-\dfrac{5}{2}\cdot1=-\dfrac{5}{2}\)
Vậy: \(A\left(1;-\dfrac{5}{2}\right)\) thuộc đồ thị hàm số y=-5/2x
b: Thay x=2 vào \(y=-\dfrac{5}{2}x\), ta được:
\(y=-\dfrac{5}{2}\cdot2=-5\)
=>B(2;-5) thuộc đồ thị hàm số y=-5/2x
Thay x=3 vào y=-5/2x, ta được:
\(y=-\dfrac{5}{2}\cdot3=-\dfrac{15}{2}\)<>7
=>\(C\left(3;7\right)\) không thuộc đồ thị hàm số y=-5/2x
Thay x=1 vào y=-5/2x, ta được:
\(y=-\dfrac{5}{2}\cdot1=-\dfrac{5}{2}\)<>5/2
=>\(D\left(1;\dfrac{5}{2}\right)\) không thuộc đồ thị hàm số \(y=-\dfrac{5}{2}x\)
Thay x=0 vào \(y=-\dfrac{5}{2}x\), ta được:
\(y=-\dfrac{5}{2}\cdot0=0\)<>4
=>E(0;4) không thuộc đồ thị hàm số \(y=-\dfrac{5}{2}x\)