tìm số nguyên x biết \(\dfrac{10+x}{17+x}=\dfrac{3}{4}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) 1/20 - (x - 8/5) = 1/10
x - 8/5 = 1/20 - 1/10
x - 8/5 = -1/20
x = -1/20 + 8/5
x = 31/20
b) 7/4 - (x + 5/3) = -12/5
x + 5/3 = 7/4 + 12/5
x + 5/3 = 83/20
x = 83/20 - 5/3
x = 149/60
c) x - [17/2 - (-3/7 + 5/3)] = -1/3
x - (17/2 - 26/21) = -1/3
x - 305/42 = -1/3
x = -1/3 + 305/42
x = 97/14

a: =>x-3=9
=>x=12
b: =>10-x=-26
=>x=36
c: =>x:4-1=2
=>x:4=3
=>x=12
d: =>x^2=4
=>x=2 hoặc x=-2
e: =>(x-2)^2=100
=>x-2=10 hoặc x-2=-10
=>x=12 hoặc x=-8

\(a,\dfrac{x}{5}=\dfrac{-18}{10}\\ \Rightarrow x=-\dfrac{18}{10}.5\\ \Rightarrow x=-9\\ b,\dfrac{6}{x-1}=\dfrac{-3}{7}\\ \Rightarrow6.7=-3\left(x-1\right)\\ \Rightarrow42=-3x+3\\ \Rightarrow42+3x-3=0\\ \Rightarrow3x+39=0\\ \Rightarrow3x=-39\\ \Rightarrow x=-13\\ c,\dfrac{y-3}{12}=\dfrac{3}{y-3}\\ \Rightarrow\left(y-3\right)^2=36\\ \Rightarrow\left[{}\begin{matrix}y-2=6\\y-2=-6\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}y=8\\y=-4\end{matrix}\right.\)
\(d,\dfrac{x}{25}=\dfrac{-5}{x^2}\\ \Rightarrow x^3=-125\\ \Rightarrow x^3=\left(-5\right)^3\\ \Rightarrow x=-5\)

a: \(\Leftrightarrow\left(x+1\right)^2=3^2=9\)
=>x+1=3 hoặc x+1=-3
=>x=2 hoặc x=-4
b: \(\Leftrightarrow\left(x-1\right)^2=16\)
=>x-1=4 hoặc x-1=-4
=>x=5 hoặc x=-3

Bài 4:
a) \(\dfrac{2.7.13}{26.35}=\dfrac{2.7.13}{13.2.7.5}=\dfrac{1}{5}\)
b) \(\dfrac{23.5-23}{4-27}=\dfrac{23.\left(5-1\right)}{-23}=\dfrac{23.4}{-23}=-4\)
c) \(\dfrac{2130-15}{3550-25}=\dfrac{2115}{3525}=\dfrac{3}{5}\)

\(a,-\dfrac{x}{2}+\dfrac{2x}{3}+\dfrac{x+1}{4}+\dfrac{2x+1}{6}=\dfrac{8}{3}\)
\(\Rightarrow-\dfrac{6x}{12}+\dfrac{8x}{12}+\dfrac{3\left(x+1\right)}{12}+\dfrac{2\left(2x+1\right)}{12}=\dfrac{8}{3}\)
\(\Rightarrow\dfrac{-6x+8x+3x+3+4x+2}{12}=\dfrac{8}{3}\)
\(\Rightarrow\dfrac{9x+5}{12}=\dfrac{8}{3}\)
\(\Rightarrow27x+15=96\)
\(\Rightarrow27x=81\)
\(\Rightarrow x=3\left(tm\right)\)
\(b,\dfrac{3}{2x+1}+\dfrac{10}{4x+2}-\dfrac{6}{6x+3}=\dfrac{12}{26}\)
\(\Rightarrow\dfrac{3}{2x+1}+\dfrac{10}{2\left(2x+1\right)}-\dfrac{6}{3\left(2x+1\right)}=\dfrac{6}{13}\)
\(\Rightarrow\dfrac{3}{2x+1}+\dfrac{5}{2x+1}-\dfrac{2}{2x+1}=\dfrac{6}{13}\)
\(\Rightarrow\dfrac{3+5-2}{2x+1}=\dfrac{6}{13}\)
\(\Rightarrow\dfrac{6}{2x+1}=\dfrac{6}{13}\)
\(\Rightarrow2x+1=13\)
\(\Rightarrow2x=12\)
\(\Rightarrow x=6\left(tm\right)\)
#Toru
a) \(-\dfrac{x}{2}+\dfrac{2x}{3}+\dfrac{x+1}{4}+\dfrac{2x+2}{6}=\dfrac{8}{3}\)
\(\Rightarrow\dfrac{-6x}{12}+\dfrac{8x}{12}+\dfrac{3\left(x+1\right)}{12}+\dfrac{2\left(2x+1\right)}{12}=\dfrac{4\cdot8}{12}\)
\(\Rightarrow-6x+8x+3x+3+4x+2=32\)
\(\Rightarrow9x+5=32\)
\(\Rightarrow9x=32-5\)
\(\Rightarrow9x=27\)
\(\Rightarrow x=\dfrac{27}{9}\)
\(\Rightarrow x=3\)
b) \(\dfrac{3}{2x+1}+\dfrac{10}{4x+2}-\dfrac{6}{6x+3}=\dfrac{12}{26}\) (ĐK: \(x\ne-\dfrac{1}{2}\))
\(\Rightarrow\dfrac{3}{2x+1}+\dfrac{10}{2\left(2x+1\right)}-\dfrac{6}{3\left(2x+1\right)}=\dfrac{6}{13}\)
\(\Rightarrow\dfrac{3}{2x+1}+\dfrac{5}{2x+1}-\dfrac{2}{2x+1}=\dfrac{6}{13}\)
\(\Rightarrow\dfrac{6}{2x+1}=\dfrac{6}{13}\)
\(\Rightarrow2x+1=13\)
\(\Rightarrow2x=12\)
\(\Rightarrow x=\dfrac{12}{2}\)
\(\Rightarrow x=6\left(tm\right)\)


a, \(\dfrac{3}{7}\)\(x\) - 0,4 = - \(\dfrac{17}{35}\)
\(\dfrac{3}{7}\)\(x\) = - \(\dfrac{17}{35}\) + 0,4
\(\dfrac{3}{7}\)\(x\) = - \(\dfrac{3}{35}\)
\(x\) = - \(\dfrac{3}{35}\): \(\dfrac{3}{7}\)
\(x\) = - \(\dfrac{1}{5}\)
b, 0,2.(\(x\) - 3) +2,4 = 10
0,2.(\(x\) - 3) = 10 - 2,4
0,2.(\(x\) - 3) = 7,6
\(x\) - 3 = 7,6:0,2
\(x\) - 3 = 38
\(x\) = 38 + 3
\(x\) = 41
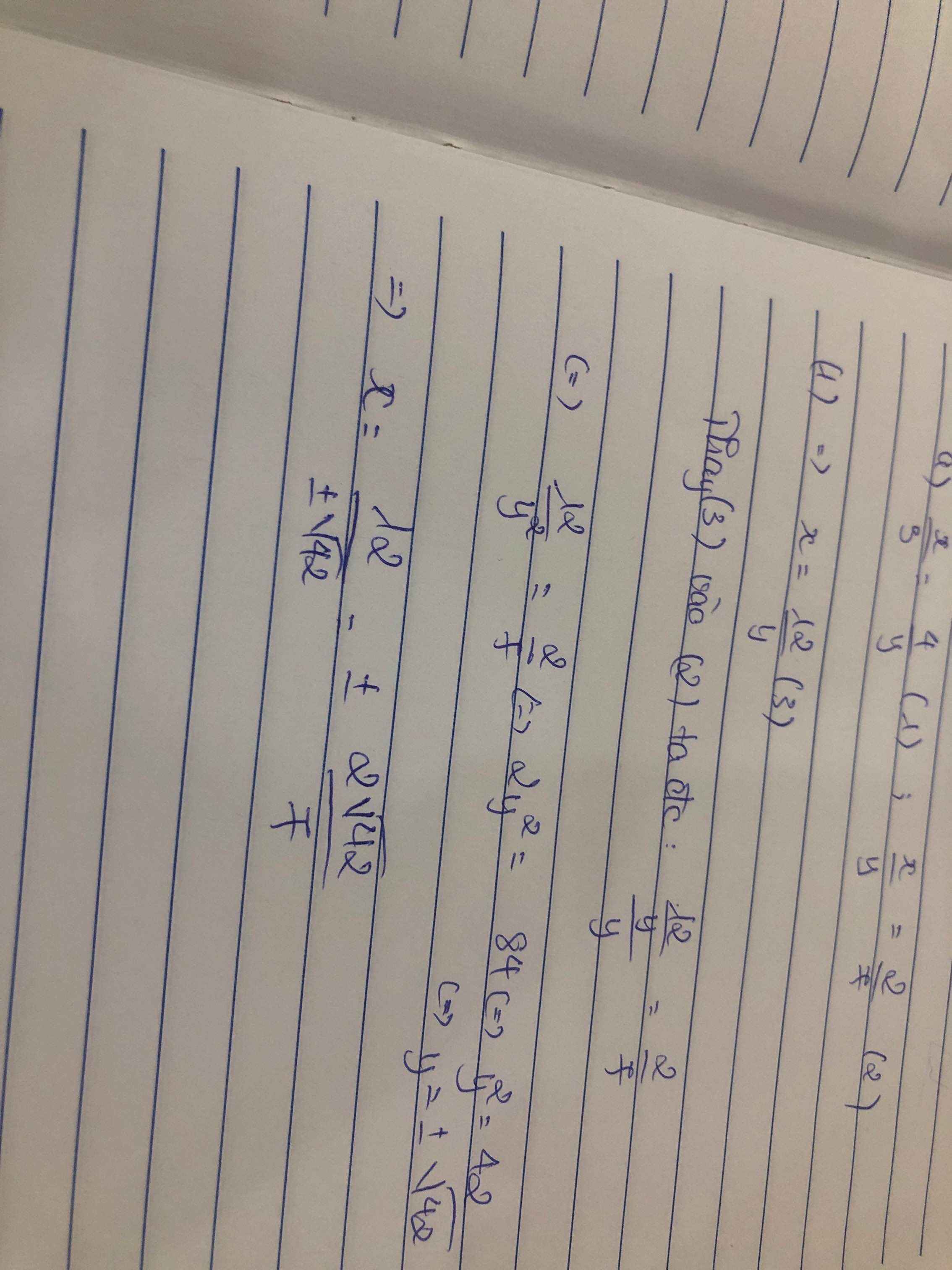
tham khảo
10+x/17+x=3/4
=>(10+x).4=(17+x).3
=>40+4x=51+3x
=>4x-3x=51-40
=>x=11
vậy:x=11 thỏa mãn đề bài
Tham khảo
10+x/17+x=3/4
=>(10+x).4=(17+x).3
=>40+4x=51+3x
=>4x-3x=51-40
=>x=11
Vậy x=11