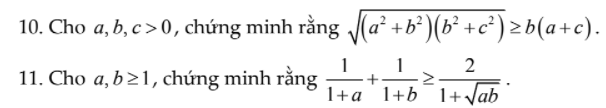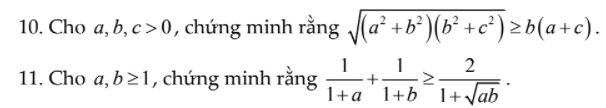S.o.S, ai giải hộ mk câu 10 với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 10 của em đây nhé:
\(\dfrac{17}{2}\) \(\times\) \(\dfrac{3}{5}\) + \(\dfrac{3}{5}\) \(\times\) \(\dfrac{1}{2}\) + \(\dfrac{3}{5}\)
= \(\dfrac{17}{2}\) \(\times\) \(\dfrac{3}{5}\) + \(\dfrac{3}{5}\) \(\times\) \(\dfrac{1}{2}\) + \(\dfrac{3}{5}\) \(\times\) 1
= \(\dfrac{3}{5}\) \(\times\) ( \(\dfrac{17}{2}\) + \(\dfrac{1}{2}\) + 1)
= \(\dfrac{3}{5}\) \(\times\) ( \(\dfrac{18}{2}\) + 1)
= \(\dfrac{3}{5}\) \(\times\) ( 9 + 1)
= \(\dfrac{3}{5}\) \(\times\) 10
= 6

10. Câu này chứng minh BĐT BSC:
\(\sqrt{\left(a^2+b^2\right)\left(b^2+c^2\right)}\ge\sqrt{\left(ab+bc\right)^2}=b\left(a+c\right)\)
11.
Ta có: \(\dfrac{1}{1+a}+\dfrac{1}{1+b}-\dfrac{2}{1+\sqrt{ab}}\)
\(=\dfrac{\left(1+b\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{\left(1+a\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2\left(1+a\right)\left(1+b\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{1+b+\sqrt{ab}+b\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{1+a+\sqrt{ab}+a\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2+2a+2b+2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{-a-b+2\sqrt{ab}+a\sqrt{ab}+b\sqrt{ab}-2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2\left(\sqrt{ab}-1\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\ge0\forall x,y\ge1\)
Đẳng thức xảy ra khi \(a=b=1\)



ĐKXĐ: ...
Với \(\left[{}\begin{matrix}x=0\\y=0\end{matrix}\right.\) ko phải nghiệm
\(\Leftrightarrow\left\{{}\begin{matrix}2-\dfrac{1}{2x+y}=\dfrac{2}{\sqrt{y}}\\2+\dfrac{1}{2x+y}=\dfrac{2}{\sqrt{x}}\end{matrix}\right.\)
Lần lượt cộng vế với vế và trừ vế cho vế 2 pt ta được:
\(\left\{{}\begin{matrix}2=\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{y}}\\\dfrac{1}{2x+y}=\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{y}}\end{matrix}\right.\)
Nhân vế với vế:
\(\dfrac{2}{2x+y}=\left(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{y}}\right)\left(\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{y}}\right)\)
\(\Leftrightarrow\dfrac{2}{2x+y}=\dfrac{1}{x}-\dfrac{1}{y}\)
\(\Leftrightarrow2x^2+xy-y^2=0\)
\(\Leftrightarrow\left(x+y\right)\left(2x-y\right)=0\)
\(\Leftrightarrow...\)

Câu 8 :B
m NaCl = 200.5% = 10(gam)
m H2O = m dd - m NaCl = 200 - 10 = 190(gam)
Câu 8:
mNaCl=5%.200=10(g)
=>mH2O=mddNaCl - mNaCl= 200-10=190(g)
=> Điều chế: Hòa tan 10 gam NaCl vào 190 gam H2O
=> CHỌN B



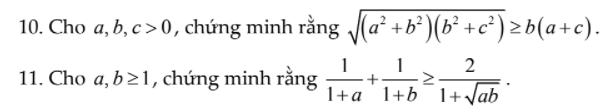 !
!