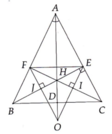
Cho tam giác ABC cân tại A ( A < 90 ° ) , đường phân giác AD. Kẻ đường cao BE, gọi H là giao điểm của BE và AD.
a) Chứng minh CH ⊥ AB .
b) Gọi F là giao điểm của CH và AB. Chứng minh AD là trung trực của EF.
c) Kẻ EI ∈ HC (I thuộc HC) , E J ∈ HB (J ∈ HB) , J ∈ H B . Chứng minh các đường thẳng EI, FJ,AD cùng đi qua một điểm, kí hiệu điểm đó là O.
d) Chứng minh AC - AF > OF - OC .
Cần gấp ạ vẽ hình càng tốt nha các bn



a: XétΔABC có
AD là đường cao
BE là đường cao
AD cắt BE tại H
Do đó: CH⊥AB
b: Ta có: ΔFBC vuông tại F
mà FD là trung tuyến
nên FD=BC/2(1)
Ta có: ΔEBC vuông tại E
mà ED là trung tuyến
nên ED=BC/2(2)
Từ (1) và (2) suy ra FD=ED(3)
Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
AB=AC
góc A chung
Do đó: ΔAEB=ΔAFC
SUy ra: AE=AF(4)
Từ (3) và (4) suy ra AD là đường trung trực của EF