Tìm a \(\in N\) để những số sau là số chín phương
1) a2+a+43
2) a2+81
3) a2+31a+1984
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DX
2
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 1 2021
a.
\(a^2+a+43=k^2\) (\(k\in N;k>a\))
\(\Leftrightarrow4a^2+4a+172=4k^2\)
\(\Leftrightarrow\left(2a+1\right)^2+171=\left(2k\right)^2\)
\(\Leftrightarrow\left(2k\right)^2-\left(2a+1\right)^2=171\)
\(\Leftrightarrow\left(2k-2a-1\right)\left(2k+2a+1\right)=171\)
Pt ước số, bạn tự lập bảng
b.
\(a^2+81=k^2\)
\(\Leftrightarrow k^2-a^2=81\)
\(\Leftrightarrow\left(k-a\right)\left(k+a\right)=81\)
Bạn tự lập bảng ước số
CM
13 tháng 9 2018
Chọn B
Cách giải: Ta có:
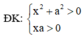
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0
ND
5 tháng 6 2019
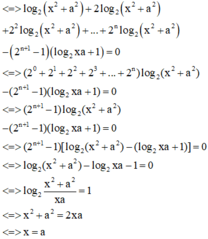
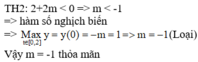
Giả sử tồn tại a thỏa mãn đề bài
Có a^2+31a+1984=x^2 (x thuộc N)
suy ra 4a^2+124a+7936=4x^2
suy ra (2a+62)^2+4092=4x^2
suy ra (2x-2a-62)(2x+2a+62)=4092
suy ra (x-a-31)(x+a+31)=1023
Từ đây bạn phân tích thành nhân tử rồi giải thôi
Chúc bạn học tốt!
5 tháng 6 2019
Em tham khảo link :
Câu hỏi của Nguyen Cao Diem Quynh - Toán lớp 8 | Học trực tuyến
10 tháng 12 2021
1:
#include <bits/stdc++.h>
using namespace std;
long long n,i,x,t;
int main()
{
cin>>n;
t=0;
for (i=1; i<=n; i++)
{
cin>>x;
t=t+x;
}
cout<<t;
return 0;
}
c. \(a^2+31a-1984=k^2\Rightarrow4a^2+124a+62^2-k^2=1528\)
\(\Rightarrow\left(2a+62\right)^2-k^2=1628\Rightarrow\left(2a+62+k\right)\left(2a+62-k\right)=1628\)
Tương tự phần trên ta tìm được \(a\in\left\{12;33;48;97;176;332;565;1728\right\}\)
a. Để \(a^2+a+43\) là số chính phương thì \(a^2+a+43=k^2\Rightarrow4a^2+4a+172=4k^2\)
\(\Rightarrow\left(4a^2+4a+1\right)-4k^2=-171\Rightarrow\left(2a+1\right)^2-4k^2=-171\)
\(\Rightarrow\left(2a+1-2k\right)\left(2a+1+2k\right)=-171\)
Vậy \(a\in\left\{2;13;42\right\}\)