cho tam giác mnp có 3 góc nhọn , 2 đường cao ni và pk cắt nhau tại h
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

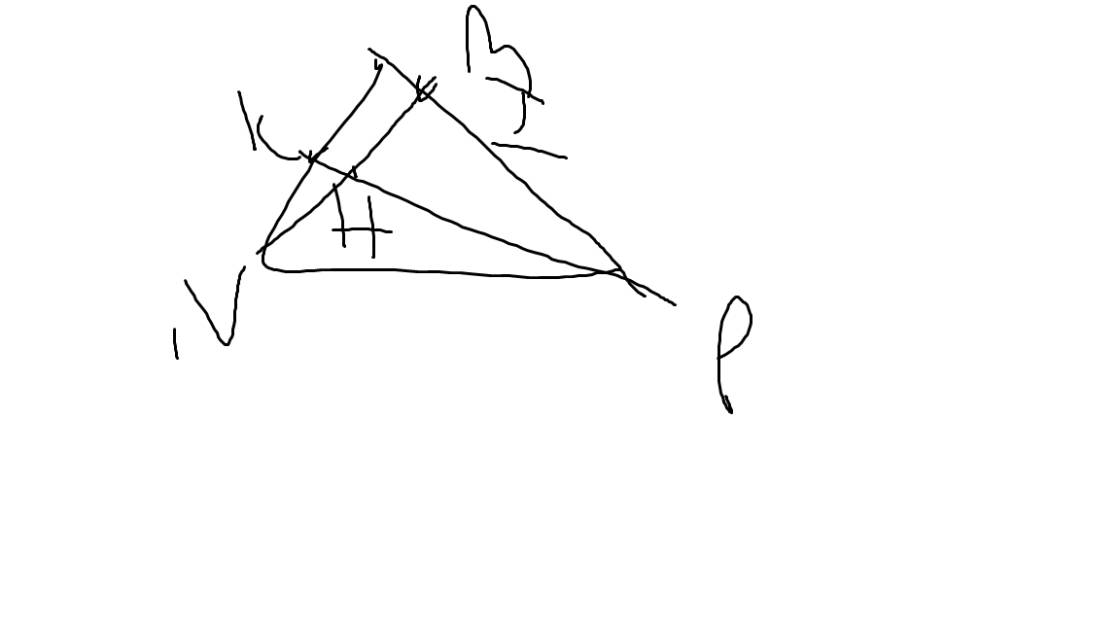

a: Xét ΔMIN vuông tại I và ΔMQP vuông tại Q có
góc M chung
=>ΔMIN đồng dạng với ΔMQP
c: Xét ΔMQI và ΔMPN có
MQ/MP=MI/MN
góc M chung
=>ΔMQI đồng dạng với ΔMPN

a) Xét ΔMNP có
NQ là đường cao ứng với cạnh MP
PR là đường cao ứng với cạnh MN
MP cắt MN tại S
Do đó: MS\(\perp\)NP
b) Ta có: MS\(\perp NP\)(cmt)
nên \(\widehat{SMN}+\widehat{MNP}=90^0\)
hay \(\widehat{SMN}=25^0\)

a: Xet ΔKNP vuông tại K và ΔHPN vuông tại H có
NP chung
góc KNP=góc HPN
=>ΔKNP=ΔHPN
b: ΔKNP=ΔHPN
=>góc ENP=góc EPN
=>ΔENP cân tại E
c: Xét ΔMKE vuông tại K và ΔMHE vuông tại H có
ME chung
MK=MH
=>ΔMKE=ΔMHE
=>góc KME=góc HME
=>ME là phân giác của góc NMP