Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Tính khoảng cách từ S tới mặt đáy (ABC).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 6 2019
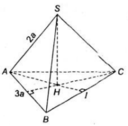
Gọi H là tâm của tam giác ABC ( khi đó H là trọng tâm, trực tâm của tam giác ABC).
Do hình chóp S.ABC là hình chóp tam giác đều nên SH ⊥ (ABC)
Vậy khoảng cách từ S đến (ABC ) là a.
CM
21 tháng 1 2018
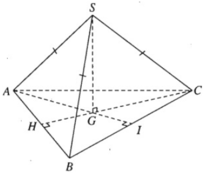
a) SG là trục đường tròn ngoại tiếp tam giác đều ABC nên SG ⊥ (ABC). Ta có
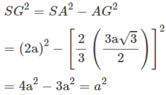
Vậy khoảng cách từ S tới mặt phẳng (ABC) là độ dài của đoạn SG = a
Ta có CG ⊥ AB tại H. Vì GH là đoạn vuông góc chung của AB và SG, do đó
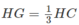
mà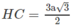 
nên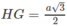 
CM
19 tháng 5 2018
Đáp án là B
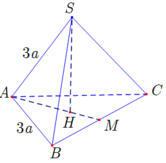
Gọi H là tâm của tam giác đều A B C ⇒ S H ⊥ A B C .
Gọi M là trung điểm của B C .
Ta có A M = 3 a 3 2 ; A H = 2 3 A M = a 3 .
Xét tam giác S A H : S H = S A 2 − A H 2 = a 6 . Vậy h = d S ; A B C = S H = a 6 .
CM
5 tháng 1 2017
Đáp án D
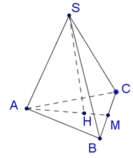
Gọi H là trọng tâm tam giác ABC, vì S.ABC là hình chóp tam giác đều nên SH vuông góc với (ABC).
Vậy . Theo bài ra ta có góc S A H ^ = 60 °
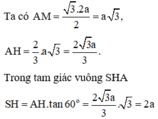
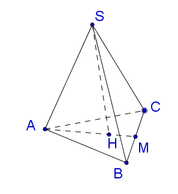
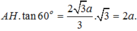
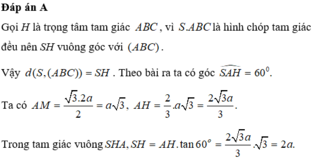
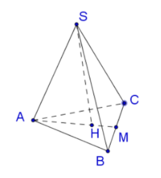
Gọi H là tâm của tam giác ABC ( khi đó H là trọng tâm, trực tâm của tam giác ABC).
Do hình chóp S.ABC là hình chóp tam giác đều nên SH ⊥ (ABC)
\(AN=\sqrt{AB^2-BN^2}\) \(=\) \(\sqrt{\left(3a\right)^2-\left(\dfrac{3a}{2}\right)^2}\) \(=\) \(\dfrac{3a\sqrt{3}}{2}\)
Vậy khoảng cách từ S đến (ABC ) là a.