Câu này giải như thế nào v ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. \(C=\dfrac{n+1}{n-2}\) \(\left(n\ne2\right)\)
\(C=\dfrac{n-2+3}{n-2}=\dfrac{n-2}{n-2}+\dfrac{3}{n-2}=1+\dfrac{3}{n-2}\)
Để C nguyên thì \(\dfrac{3}{n-2}\in Z\) \(\Leftrightarrow n-2\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
`@n-2=1->n=3(n)`
`@n-2=-1->n=1(n)`
`@n-2=3->n=5(n)`
`@n-2=-3->n=-1(n)`
Vậy \(n\in\left\{3;1;5;-1\right\}\) thì C nguyên
b.\(D=\dfrac{2n+1}{5n-3}\left(n\ne\dfrac{3}{5}\right)\)
Ta có: \(2n+1⋮5n-3\)
\(\Leftrightarrow5.\left(2n+1\right)⋮\left(5n-3\right)\)
\(\Leftrightarrow10n+5⋮5n-3\)
\(\Leftrightarrow2\left(5n-3\right)+11⋮\left(5n-3\right)\)
Vì \(2\left(5n-3\right)⋮\left(5n-3\right)\) nên để D nguyên thì \(11⋮\left(5n-3\right)\)
hay \(5n-3\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
`@5n-3=1->n=14/5(l)`
`@5n-3=-1->n=2/5(l)`
`@5n-3=11->n=14/5(l)`
`@5n-3=-11->n=-8/5(l)`
Vậy không có giá trị \(n\in Z\) thỏa mãn

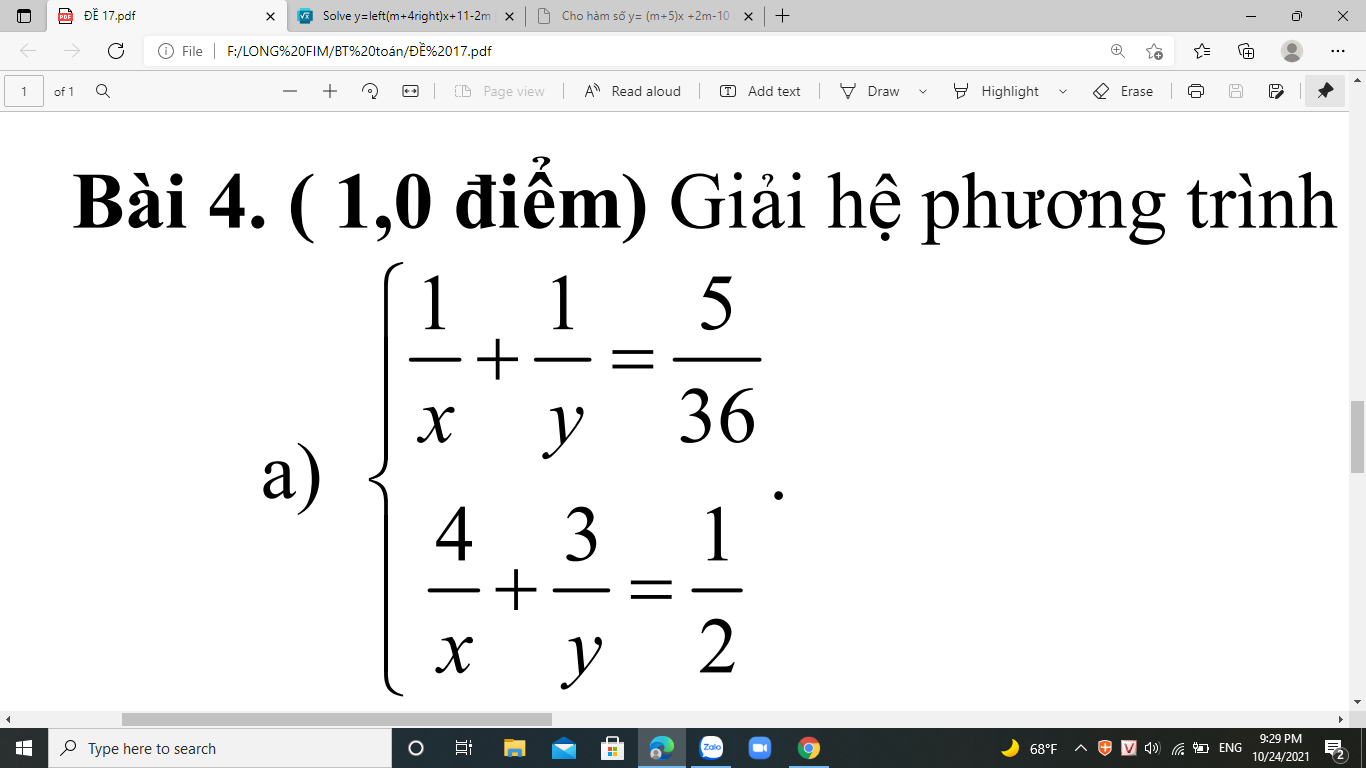
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{5}{36}\\\dfrac{4}{x}+\dfrac{3}{y}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{4}{y}=\dfrac{5}{9}\\\dfrac{4}{x}+\dfrac{3}{y}=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{y}=\dfrac{1}{18}\\\dfrac{1}{x}=\dfrac{1}{36}-\dfrac{1}{18}=-\dfrac{1}{36}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=18\\x=-36\end{matrix}\right.\)

Với \(n\in N;n>0\) có:
\(\dfrac{1}{\left(n+1\right)\sqrt{n}+n\sqrt{n+1}}=\dfrac{1}{\sqrt{n\left(n+1\right)}\left(\sqrt{n+1}+\sqrt{n}\right)}=\dfrac{\sqrt{n+1}-\sqrt{n}}{\sqrt{n\left(n+1\right)}\left(n+1-n\right)}=\dfrac{1}{\sqrt{n}}-\dfrac{1}{\sqrt{n+1}}\)
Áp dụng vào P có:
\(P=1-\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{2016}}-\dfrac{1}{\sqrt{2017}}\)
\(=1-\dfrac{1}{\sqrt{2017}}\)
\(\Rightarrow a^2+b=1^2+2017=2018\)
Ý A




3: Gọi I là điểm đối xứng của O qua BC, OI cắt BC tại N
=>N là trung điểm chung của OI và BC và I,N cố định
BH//CD; CH//BD
=>BHCD là hbh
=>N là trung điểm của HD
ON là đường trung bình của ΔAHD
=>AH=2ON
=>AH=OI=2ON
AH//OI
=>AHOI là hbh
=>IH=OA=R
=>H thuộc (I;R) cố định
 giải câu này như thế nào ạ
giải câu này như thế nào ạ

Lọ 1 : AgNO3
\(AgNO_3 + KI \to AgI + KNO_3\\ AgNO_3 + HCl \to AgCl + HNO_3\\ 2AgNO_3 + Na_2CO_3 \to 2NaNO_3 + Ag_2CO_3\)
Lọ 2 : KI
Lọ 3 : Na2CO3
\(Na_2CO_3 + 2HCl \to 2NaCl + CO_2 + H_2O\\ \)
Lọ 4 : HCl