Vẽ \(\Delta\)ABC. Giả sử govs B=350, góc C=550. \(\Delta\) ABC là tam giác gì
ai nhanh mik cho 3k
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LB
18 tháng 2
vì BI là tia phân giác của ^ABC => ^ ABI = ^ IBC= ^ ABC / 2 = 80 / 2 =40
=>^IBC=40
vì CI là tia phân giác của ^ACB => ^ACI = ^ ICB = ACB / 2 = 40 / 2 = 20
=>^ICB = 20
Ta có : ^BIC+^IBC+^ICB= 180 ( tổng ba góc của 1 tam giác )
=> ^BIC +40+20 =180
=>^BIC = 120
29 tháng 2 2016
a)xét tam gác ABD và EBD có
góc ABP=EBP
PB là cạnh chung
góc A=E=90độ
ABD = EBD(cạnh huyền góc nhọn)
1 tháng 10 2016
Đường cao AH vuông góc với BC tại H,HI vuông góc AC tại I
=>\(\Delta AHI,\Delta AHC\)có\(90^0=\widehat{A}+\widehat{AHI}=\widehat{A}+\widehat{C}\Rightarrow\widehat{AHI}=\widehat{C}\)
\(\Delta ABC\)có\(\widehat{C}=180^0-\widehat{B}-\widehat{BAC}=180^0-75^0-65^0=40^0\)mà\(\widehat{AHI}=\widehat{C}\left(cmt\right)\Rightarrow\widehat{AHI}=40^0\)
12 tháng 1 2022
\(\widehat{B}+\widehat{C}=140^0\)
\(\Leftrightarrow4\cdot\widehat{C}=140^0\)
\(\Leftrightarrow\widehat{C}=35^0\)
hay \(\widehat{B}=105^0\)
Vậy: ΔABC tù
22 tháng 2 2023
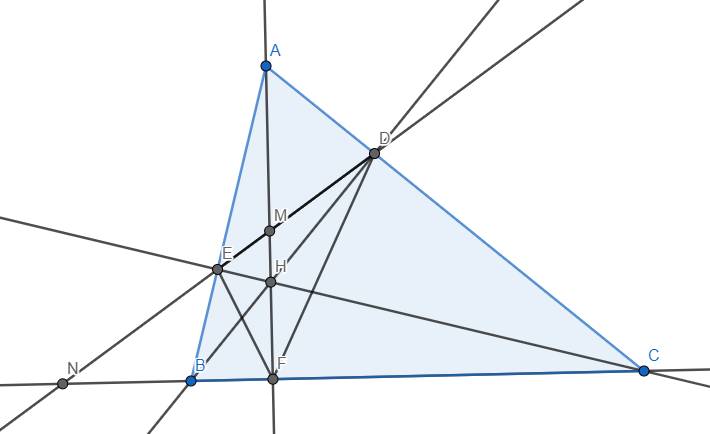
a) Xét \(\Delta ABD\) và \(\Delta ACE\), ta có \(\widehat{ADB}=\widehat{AEC}\left(=90^o\right)\) và góc A chung \(\Rightarrow\Delta ABD~\Delta ACE\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\) \(\Rightarrowđpcm\)
b) Từ \(AE.AB=AD.AC\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét \(\Delta ADE\) và \(\Delta ABC\), ta có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\) và góc A chung \(\Rightarrowđpcm\)
c) Do \(\Delta ADE~\Delta ABC\) \(\Rightarrow\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{AD}{AB}\right)^2\)
Lại có \(\dfrac{AD}{AB}=cosA=cos45^o=\dfrac{1}{\sqrt{2}}\) nên \(\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{1}{\sqrt{2}}\right)^2=\dfrac{1}{2}\)\(\Rightarrow\dfrac{S_{ADE}}{S_{ABC}-S_{ADE}}=\dfrac{1}{2-1}\) \(\Rightarrow\dfrac{S_{ADE}}{S_{BEDC}}=1\)
d) Kẻ đường cao AF của tam giác ABC. Tương tự câu b, ta chứng minh được các tam giác BFE và CDF cùng đồng dạng với tam giác ABC. Từ đó suy ra \(\Delta BEF~\Delta DCF\) \(\Rightarrow\widehat{BFE}=\widehat{CFD}\) \(\Rightarrow90^o-\widehat{BFE}=90^o-\widehat{CFD}\) \(\Rightarrow\widehat{EFM}=\widehat{DFM}\) \(\Rightarrow\) FM là tia phân giác trong tam giác DEF \(\Rightarrow\dfrac{MD}{ME}=\dfrac{FD}{FE}\).
Mặt khác, \(FN\perp FM\) \(\Rightarrow\) FN là phân giác ngoài của tam giác DEF \(\Rightarrow\dfrac{ND}{NE}=\dfrac{FD}{FE}\). Từ đó suy ra \(\dfrac{MD}{ME}=\dfrac{ND}{NE}\) \(\Rightarrowđpcm\)
7 tháng 5 2021
Xin lỗi mấy bạn . Mình bị thiếu chỗ (cho tam giác ABC vuông tại A)
Số đo góc A:
180-35-55=90 (độ)
Vì: tam giác ABC có 1 trong 3 góc tạo thành có 1 góc bằng 90 độ.
=> Tam giác ABC là tam giác vuông tại đỉnh A.
ta có góc B + góc C +góc A = 180 độ
=> góc A =180 độ - góc B - góc C
= 180 độ - 35 độ - 55 độ
= 90 độ
Vậy tam giác ABC là tam giác vuông