Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) tam giác ABC vuông tại A
=> AB2 + AC2 = BC2 (định lý py-ta-go)
=> 92 + AC2 = 152
=> AC2 = 225 - 81
=> AC2 = 144 => AC = \(\sqrt{144}=12cm\)
t i c k đúng nhé
a) trong tam giác ABC có: AB < AC < BC ( 9 < 12 < 15)
=> góc C < góc B < góc A (định lý)

hình như đề sai thì phải tia đối của AC là Ax mà sao tia phân giác của góc BAx lại cặt BC tại E được

A B C M N H E D I I
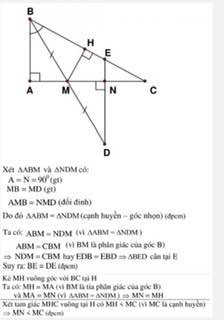
Xét \(\Delta ABM\)và \(\Delta NDM\)có: \(\hept{\begin{cases}\widehat{A}=\widehat{DNM}=90^o\left(gt\right)\\MB=MD\left(gt\right)\\\widehat{AMB}=\widehat{NMD}\end{cases}}\Rightarrow\Delta ABM=\Delta NDM\left(ch-gn\right)\left(đpcm\right)\)
Ta có \(\widehat{ABM}=\widehat{NDM}\left(\Delta ABM=\Delta NDM\right)\)
\(\widehat{ABM}=\widehat{CBM}\)(BM là phân giác \(\widehat{B}\))
\(\Rightarrow\widehat{NDM}=\widehat{CBM}\)hay \(\widehat{EDB}=\widehat{EBD}\)
\(\Rightarrow\Delta BED\)cân tại E
=> BE=DE (đpcm)
Kẻ MH vuông góc với BC tại H
Ta có MH=MA (vì BM là tia phân giác của \(\widehat{B}\))
và MA=MN (\(\Delta ABM=\Delta NDM\))
=> MN=MH
Xét \(\Delta MHC\)vuông tại H có MH<MC (vì MC là cạnh huyền)
=> MN<MC (đpcm)

a) Xét 2 tam giác vuông: \(\Delta ABD\)và \(\Delta EBD\)có:
\(BD:\)cạnh chung
\(\widehat{ABD}=\widehat{EBD}\)(gt)
suy ra: \(\Delta ABD=\Delta EBD\)(ch_gn)
b) \(\Delta ABD=\Delta EBD\)
\(\Rightarrow\)\(AB=EB\)(cạnh tương ứng)
\(\Rightarrow\)\(\Delta ABE\)cân tại \(A\)
mà \(\widehat{ABE}=60^0\)
\(\Rightarrow\)\(\Delta ABE\)là tam giác đều

B tham khảo lời giải trong này xemm https://cunghocvui.com/danh-muc/toan-lop-7
a)xét tam gác ABD và EBD có
góc ABP=EBP
PB là cạnh chung
góc A=E=90độ
ABD = EBD(cạnh huyền góc nhọn)
Là tam giác cân đấy bạn!