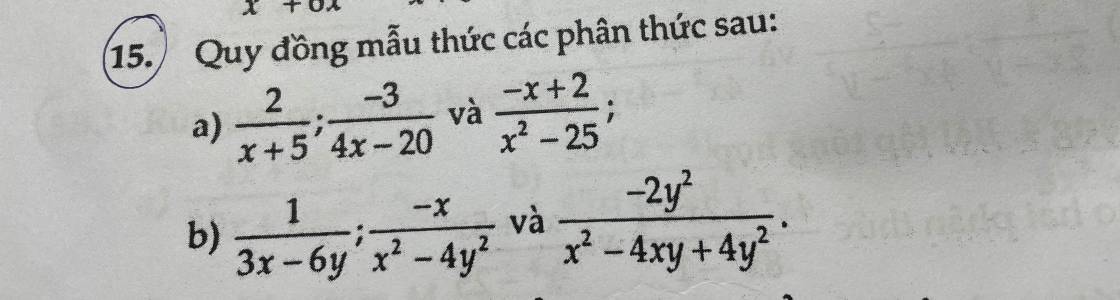Giúp em điiiiiiii🥲
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(72.\)
Xét tam giác AHC vuông tại H ta có:
\(\sin C=\dfrac{AH}{AC}\) (Tỉ số lượng giác).
\(\Rightarrow\sin30^o=\dfrac{AH}{40}.\Rightarrow AH=20.\)
Xét tam giác AHB vuông tại H:
\(AB^2=AH^2+BH^2\left(Pytago\right).\)
\(\Rightarrow29^2=20^2+BH^2.\\ \Leftrightarrow BH^2=29^2-20^2.\\ \Rightarrow BH=21.\)

Gọi vận tốc xe 1 và xe 2 lần lượt là a,b
Theo đề, ta có:
1/4a=1/3b và 1,6(a+b)=112
=>a=40; b=30

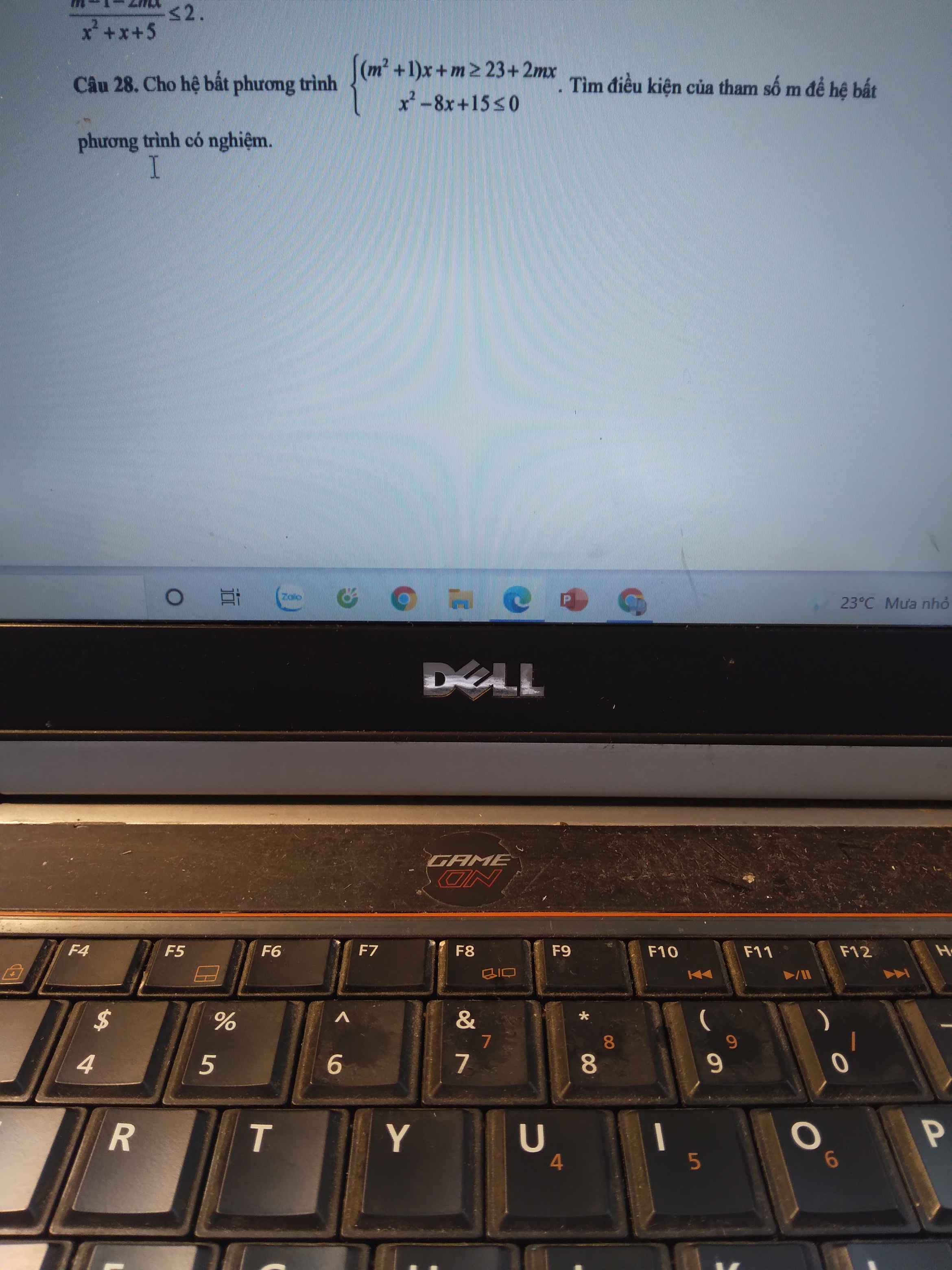
Xét BPT: \(x^2-8x+15\le0\Leftrightarrow3\le x\le5\Rightarrow D_1=\left[3;5\right]\)
Xét BPT: \(\left(m^2+1\right)x+m\ge23+2mx\)
\(\Leftrightarrow\left(m^2-2m+1\right)x\ge23-m\)
\(\Leftrightarrow\left(m-1\right)^2x\ge23-m\) (1)
- Với \(m=1\Rightarrow\left(1\right)\) trở thành \(0\ge22\) (vô lý) \(\Rightarrow\left(1\right)\) vô nghiệm (loại)
- Với \(m\ne1\Rightarrow\left(m-1\right)^2>0;\forall m\)
\(\left(1\right)\Leftrightarrow x\ge\dfrac{23-m}{\left(m-1\right)^2}\) \(\Rightarrow D_2=\left[\dfrac{23-m}{(m-1)^2};+\infty \right)\)
Hệ đã cho có nghiệm khi và chỉ khi \(D_1\cap D_2\ne\varnothing\)
\(\Rightarrow\dfrac{23-m}{\left(m-1\right)^2}\le5\)
\(\Leftrightarrow23-m\le5\left(m-1\right)^2\)
\(\Leftrightarrow5m^2-9m-18\ge0\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-\dfrac{6}{5}\end{matrix}\right.\)


a: \(\dfrac{2}{x+5}=\dfrac{2\cdot4\cdot\left(x-5\right)}{4\left(x-5\right)\left(x+5\right)}=\dfrac{8\left(x-5\right)}{4\left(x-5\right)\left(x+5\right)}\)
\(\dfrac{-3}{4x-20}=\dfrac{-3}{4\left(x-5\right)}=\dfrac{-3\left(x+5\right)}{4\left(x-5\right)\left(x+5\right)}=\dfrac{-3x-15}{4\left(x-5\right)\left(x+5\right)}\)
\(\dfrac{-x+2}{x^2-25}=\dfrac{-x+2}{\left(x-5\right)\left(x+5\right)}=\dfrac{4\left(-x+2\right)}{4\left(x-5\right)\left(x+5\right)}=\dfrac{-4x+8}{4\left(x-5\right)\left(x+5\right)}\)
b: \(\dfrac{1}{3x-6y}=\dfrac{1}{3\left(x-2y\right)}=\dfrac{\left(x-2y\right)\left(x+2y\right)}{3\left(x-2y\right)^2\cdot\left(x+2y\right)}\)
\(\dfrac{-x}{x^2-4y^2}=\dfrac{-x}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{-x\cdot3\cdot\left(x-2y\right)}{3\left(x-2y\right)^2\cdot\left(x+2y\right)}\)
\(\dfrac{-2y^2}{x^2-4xy+4y^2}=\dfrac{-2y^2}{\left(x-2y\right)^2}=\dfrac{-2y^2\cdot3\left(x+2y\right)}{3\left(x+2y\right)\left(x-2y\right)^2}\)
\(=\dfrac{-6y^2\left(x+2y\right)}{3\left(x+2y\right)\left(x-2y\right)^2}\)


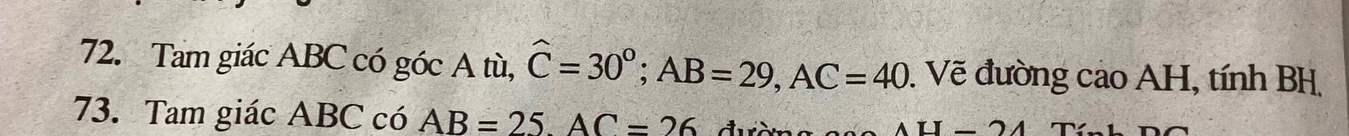 bài 72 giúp em 🥲🥲
bài 72 giúp em 🥲🥲