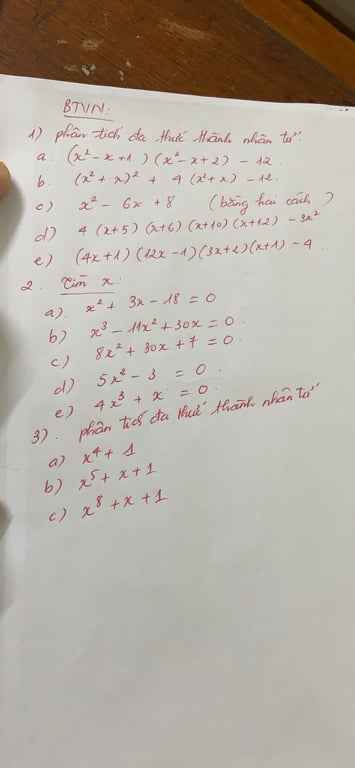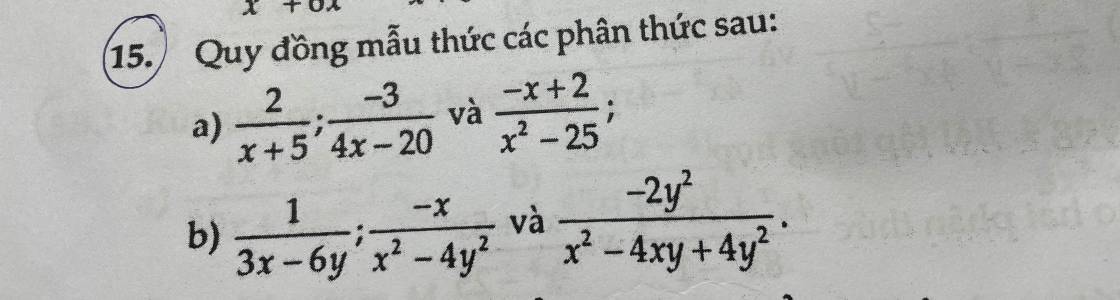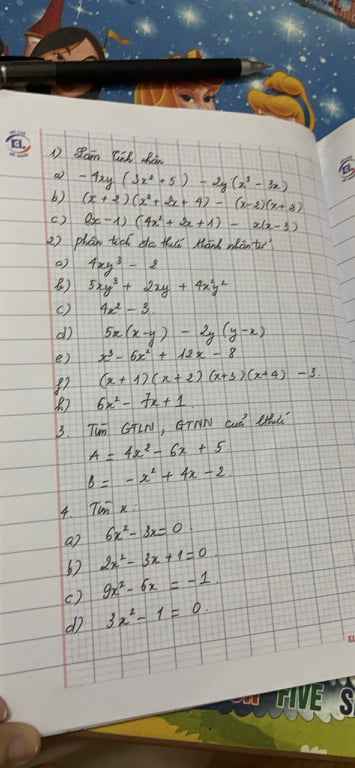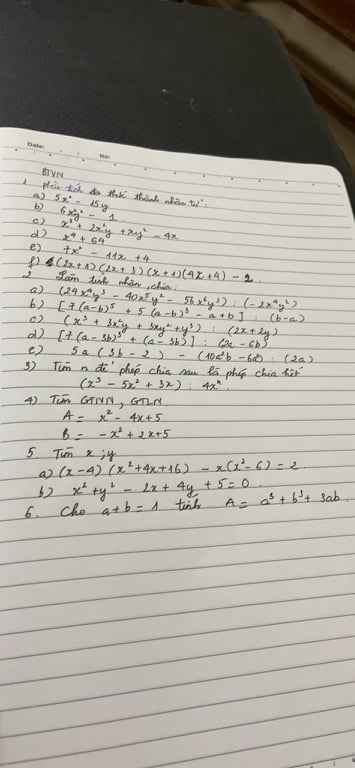Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
a) \(x^4+4\)
\(=x^4+4x^2+4-4x^2\)
\(=\left(x^2+2\right)^2-\left(2x\right)^2\)
\(=\left(x^2-2x+2\right)\left(x^2+2x+2\right)\)
b) \(x^5+x+1\)
\(=x^5+x^4+x^3-x^4-x^3-x^2+x^2+x+1\)
\(=x^3\left(x^2+x+1\right)-x^2\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^3-x^2+1\right)\)
c) \(x^8+x+1\)
\(=x^8+x^7+x^6-x^7-x^6-x^5+x^5+x^4+x^3-x^4-x^3-x^2+x^2+x+1\)
\(=x^6\left(x^2+x+1\right)-x^5\left(x^2+x+1\right)+x^3\left(x^2+x+1\right)-x^2\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^6-x^5+x^3-x^2+1\right)\)
Bài 1:
a) \(\left(x^2-x+1\right)\left(x^2-x+2\right)-12\)
\(=\left(x^2-x\right)^2+3\left(x^2-x\right)+2-12\)
\(=\left(x^2-x\right)^2+5\left(x^2-x\right)-2\left(x^2-x\right)-10\)
\(=\left(x^2-x\right)\left(x^2-x+5\right)-2\left(x^2-x+5\right)\)
\(=\left(x^2-x+5\right)\left(x^2-x-2\right)\)
\(=\left(x-2\right)\left(x+1\right)\left(x^2-x+5\right)\)
b) \(\left(x^2+x\right)^2+4\left(x^2+x\right)-12\)
\(=\left(x^2+x\right)^2+6\left(x^2+x\right)-2\left(x^2+x\right)-12\)
\(=\left(x^2+x+6\right)\left(x^2+x-2\right)\)
\(=\left(x+2\right)\left(x-1\right)\left(x^2+x+6\right)\)
c) \(x^2-6x+8\)
\(=x^2-6x+9-1\)
\(=\left(x-3\right)^2-1\)
\(=\left(x-4\right)\left(x-2\right)\)

a: \(\dfrac{2}{x+5}=\dfrac{2\cdot4\cdot\left(x-5\right)}{4\left(x-5\right)\left(x+5\right)}=\dfrac{8\left(x-5\right)}{4\left(x-5\right)\left(x+5\right)}\)
\(\dfrac{-3}{4x-20}=\dfrac{-3}{4\left(x-5\right)}=\dfrac{-3\left(x+5\right)}{4\left(x-5\right)\left(x+5\right)}=\dfrac{-3x-15}{4\left(x-5\right)\left(x+5\right)}\)
\(\dfrac{-x+2}{x^2-25}=\dfrac{-x+2}{\left(x-5\right)\left(x+5\right)}=\dfrac{4\left(-x+2\right)}{4\left(x-5\right)\left(x+5\right)}=\dfrac{-4x+8}{4\left(x-5\right)\left(x+5\right)}\)
b: \(\dfrac{1}{3x-6y}=\dfrac{1}{3\left(x-2y\right)}=\dfrac{\left(x-2y\right)\left(x+2y\right)}{3\left(x-2y\right)^2\cdot\left(x+2y\right)}\)
\(\dfrac{-x}{x^2-4y^2}=\dfrac{-x}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{-x\cdot3\cdot\left(x-2y\right)}{3\left(x-2y\right)^2\cdot\left(x+2y\right)}\)
\(\dfrac{-2y^2}{x^2-4xy+4y^2}=\dfrac{-2y^2}{\left(x-2y\right)^2}=\dfrac{-2y^2\cdot3\left(x+2y\right)}{3\left(x+2y\right)\left(x-2y\right)^2}\)
\(=\dfrac{-6y^2\left(x+2y\right)}{3\left(x+2y\right)\left(x-2y\right)^2}\)

a) 4xy3-2=2(2xy3-1)
b) 5xy3+2xy+4x2y2=xy(5y2+2+4xy)
d) 5x(x-y)-2y(y-x)=(5x+2y)(x-y)
e) x3-6x2+12x-8=(x-2)3
f) (x+1)(x+2)(x+3)(x+4)-3=\(\left[\left(x+1\right)\left(x+4\right)\right]\left[\left(x+2\right)\left(x+3\right)\right]-3\)=\(\left(x^2+5x+4\right)\left(x^2+5x+6\right)-3\)
Đặt x2+5x+5=y
\(\left(x^2+5x+4\right)\left(x^2+5x+6\right)-3\)
= (y-1)(y+1)-3
=y2-1-3
=y2-4
=(y-2)(y+2)
= (x2+5x+5-2)(x2+5x+5+2)
= (x2+5x+3)(x2+5x+7)
h) 6x2-7x+1=(6x2-6x)-(x-1)=6x(x-1)-(x-1)=(6x-1)(x-1)


14: \(=\dfrac{4x+7+1}{\left(x+2\right)\left(4x+7\right)}=\dfrac{4}{4x+7}\)

14:
a: Xét ΔHNM vuông tại H và ΔMNP vuông tại M có
góc N chung
=>ΔHNM đồng dạng với ΔMNP
b: NP=căn 3^2+4^2=5cm
MH=3*4/5=2,4cm
NH=3^2/5=1,8cm
13:
a: 3x+5=x-5
=>2x=-10
=>x=-5
b: (x-2)(2x+5)=0
=>x-2=0 hoặc 2x+5=0
=>x=2 hoặc x=-5/2
c: =>2(5x-2)=3(3x+1)
=>10x-4=9x+3
=>x=7
d: =>(3x+6-x+1)/(x+2)(x-1)=17-3x/(x+2)(x-1)
=>2x+7=17-3x
=>5x=10
=>x=2

a: \(\left(x-3\right)\left(2x^2-3x+4\right)\)
\(=2x^3-3x^2+4x-6x^2+9x-12\)
\(=2x^3-9x^2+13x-12\)
b: \(\left(4x^2y-5xy^2+6xy\right):2xy\)
\(=\dfrac{4x^2y-5xy^2+6xy}{2xy}\)
\(=\dfrac{2xy\cdot2x-2xy\cdot2,5y+2xy\cdot3}{2xy}\)
\(=2x-2,5y+3\)
c: \(\dfrac{x}{2x+4}-\dfrac{2}{x^3+2x}\)
\(=\dfrac{x\left(x^3+2x\right)-2\left(2x+4\right)}{x\left(x^2+2\right)\cdot2\cdot\left(x+2\right)}\)
\(=\dfrac{x^4+2x^2-4x-8}{2x\left(x^2+2\right)\left(x+2\right)}\)

a: Xét tứ giác ABCM có
AB//CM
AB=CM
Do đó: ABCM là hình bình hàn
Suy ra: AM//BC

Những câu dạng như 19 hoặc 20 thì em nên sử dụng phương pháp trắc nghiệm chứ ko nên giải tự luận (vì như thế quá tồn thời gian, 1 bài kiểm tra trắc nghiệm ko đủ thời gian cho phép làm điều đó)
Câu 19 thử A, C đều sai, B cũng sai do ko phù hợp ĐKXĐ, do đó D đúng
Câu 20 tương tự, thử với \(x=-1\) thỏa mãn, \(x=3;x=4\) đều ko thỏa mãn, vậy A đúng
21A
22B
23A
24A
25C
26A
27C
28A