Ghi đầy đủ giúp em ạ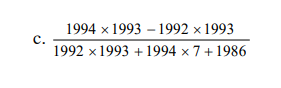
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 6 2021
`D=(a+4sqrta+4)/(sqrta+2)+(4-a)/(sqrta-2)`
`=(sqrta+2)^2/(sqrta+2)+((2-sqrta)(2+sqrta))/(sqrta-2)`
`=sqrta+2-(2+sqrta)`
`=0`
TG
26 tháng 6 2021
ĐK: a ≥ 0; a khác 4
\(D=\dfrac{a+\sqrt{a}+4}{\sqrt{a}+2}+\dfrac{\left(2-\sqrt{a}\right)\left(2+\sqrt{a}\right)}{\sqrt{a}-2}\)
\(=\dfrac{a+\sqrt{a}+4}{\sqrt{a}+2}-\left(2+\sqrt{a}\right)\)
\(=\dfrac{\left(a+\sqrt{a}+4\right)-\left(2+\sqrt{a}\right)^2}{\sqrt{a}+2}=\dfrac{a+\sqrt{a}+4-\left(4+4\sqrt{a}+a\right)}{\sqrt{a}+2}=\dfrac{a+\sqrt{a}+4-4-4\sqrt{a}-a}{\sqrt{a}+2}=-\dfrac{3}{\sqrt{a}}\)
NK
)
6
NK
5
ML
0
TP
6
BC
15 tháng 3 2022
\(\dfrac{24}{-4}\le x< \dfrac{-14}{7}\)
\(=\dfrac{-24}{4}\le x< \dfrac{-14}{7}\)
\(=-6\le x< -2\)
\(\Rightarrow\) x \(\in\) {-6;-5;-4;-3}
Vậy chọn B
17 tháng 12 2022
\(=\dfrac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}+1\right)}\)
\(=\dfrac{a+\sqrt{a}+1-a+\sqrt{a}-1}{\sqrt{a}}=\dfrac{2\sqrt{a}}{\sqrt{a}}=2\)
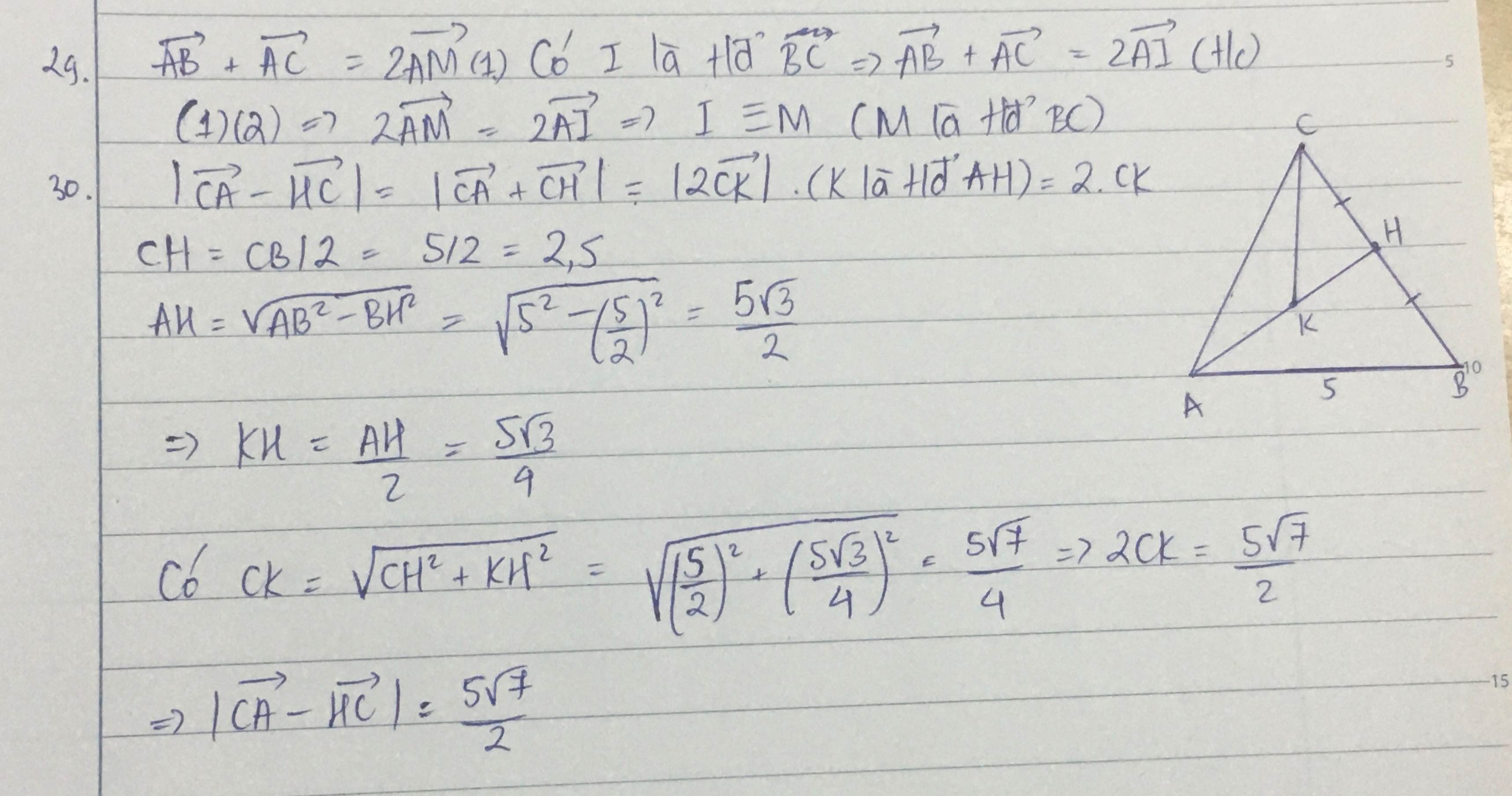
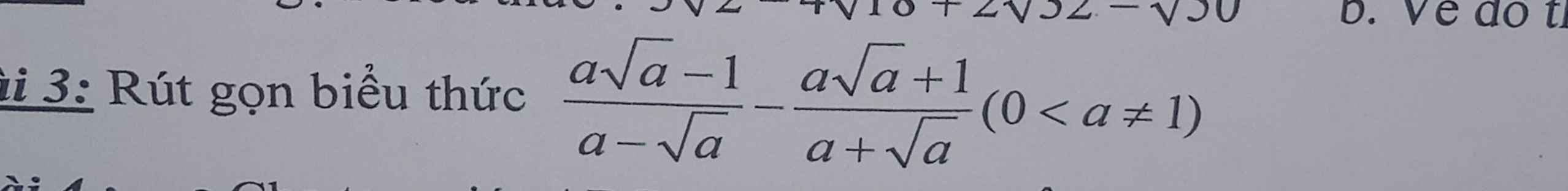
trình bày đầy đủ giúp em ạ
1/1000
\(=\dfrac{1993}{7+1986}=\dfrac{1993}{1993}=1\)