A B E C D Đề xuất bài toán tổng quát chứng minh AB song song với...
Đọc tiếp
Đề xuất bài toán tổng quát chứng minh AB song song với CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
20 tháng 7 2023
Bài 5
\(\widehat{A}+\widehat{D}=180^o\) (Hai góc trong cùng phía bù nhau)
\(\widehat{DAx}=\widehat{BAx}=\dfrac{\widehat{A}}{2}\) (gt)
\(\widehat{ADy}+\widehat{CDy}=\dfrac{\widehat{D}}{2}\) (gt)
\(\Rightarrow\widehat{DAx}+\widehat{ADy}=\dfrac{\widehat{A}}{2}+\dfrac{\widehat{D}}{2}=\dfrac{180^o}{2}=90^o\)
Xét tg ADE có
\(\widehat{AED}=180^o-\left(\widehat{DAx}+\widehat{ADy}\right)=180^o-90^o=90^o\) (Tổng các góc trong của tg bằng 180 độ)
\(\Rightarrow Ax\perp Dy\)
Bài 6:
a/
Ta có
AB//CD => AB//DE
BE//AB (gt)
=> ABED là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
=> AB = DE; AD = BE (Trong hình bình hành các cạnh đối nhau thì bằng nhau)
b/
CD - DE = CE
Mà AB = DE (cmt)
=> CD - AB = CE
c/
Xét tg BCE có
BC+BE>CE (trong tg tổng độ dài 2 cạnh lớn hơn độ dài cạnh còn lại)
Mà CE = CD - DE và DE = AB (cmt) và BE = AD
=> BC+BE = BC + AD>CE = CD - AB
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
20 tháng 7 2023
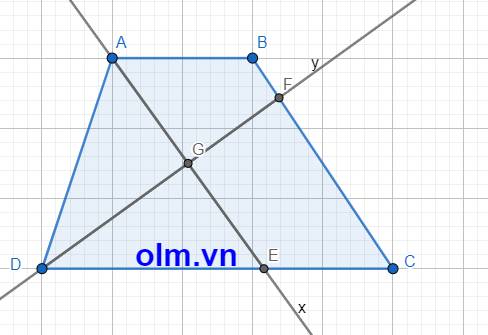
Gọi G là giao điểm của hai đường phân giác Ax và By
Ta có: \(\widehat{ADG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) ( vì DG là phân giác góc ADE)
\(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{DAB}\)( vì AG là phân giác góc DAB )
⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) + \(\dfrac{1}{2}\)\(\widehat{DAB}\) = \(\dfrac{1}{2}\)(\(\widehat{ADE}\) + \(\widehat{DAB}\))
\(\widehat{ADE}\) + \(\widehat{DAB}\) = 1800 (vì hai góc là hai góc trong cùng phía)
⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\) \(\times\) 1800 = 900
Xét tam giác ADG có: \(\widehat{GAD}\) + \(\widehat{ADG}\) + \(\widehat{DGA}\) = 1800 (tổng ba góc trong 1 tam giác bằng 1800)
⇒ \(\widehat{DGA}\) = 1800 - 900 = 900
Vậy tam giác ADG vuông tại G ⇒AE \(\perp\) DG (đpcm)
TN
0
CM
22 tháng 5 2017
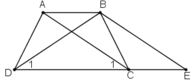
a) Hình thang ABEC (AB//CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó ΔBDE cân
Vậy hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
20 tháng 9 2019
a) Hình thang ABEC (AB//CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó \(\Delta BDE\) cân
b ) Ta có : AC // BE
\(\Rightarrow\widehat{C}_1=\widehat{E}\) ( 3 )
Tam giác BDE cân tại B ( câu a ) nên \(\widehat{D}_1=\widehat{E}\) ( 4 )
Từ (3 ) và ( 4 ) \(\Rightarrow\widehat{C}_1=\widehat{D}_1\)
Xét \(\Delta ACD\) và \(\Delta BCD\) có AC = CD ( gt )
\(\widehat{C}_1=\widehat{D}_1\left(cmt\right)\)
CD là cạnh chung
Nên \(\Delta ACD=\Delta BCD\left(c.g.c\right)\)
c ) Vì \(\Delta ACD=\Delta BCD\) ( câu b ) \(\Rightarrow\widehat{ADC}=\widehat{BCD}\)
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Chúc bạn học tốt !!!
C
10 tháng 10 2020
1) Chứng minh định lí “Hình thang có hai đường chéo bằng nhau là hình thang cân” qua bài toán sau : Cho hình thang ABCD(AB//CD)ABCD(AB//CD) có AC=BDAC=BD. Qua BB kẻ đường thẳng song song với ACAC, cắt đường thẳng DCDC tại EE. Chứng minh rằng:
a) BDEBDE là tam giác cân.
b) △ACD=△BDC.△ACD=△BDC.
c) Hình thang ABCDABCD là hình thang cân.
chúc hok tốt , k nha! sai cũng k
14 tháng 12 2021
Cm: a) Ta có: BA ⊥⊥AC (gt)
HD // AB (gt)
=> HD ⊥⊥AC => ˆHDA=900HDA^=900
Ta lại có: AC ⊥⊥AB (gt)
HE // AC (gt)
=> HE ⊥⊥AB => ˆHEA=900HEA^=900
Xét tứ giác AEHD có: ˆA=ˆAEH=ˆHDA=900A^=AEH^=HDA^=900
=> AEHD là HCN => AH = DE
b) Gọi O là giao điểm của AH và DE
Ta có: AEHD là HCN => OE = OH = OD = OA
=> t/giác OAD cân tại O => ˆOAD=ˆODAOAD^=ODA^ (1)
Xét t/giác ABC vuông tại A có AM là đường trung tuyến
-> AM = BM = MC = 1/2 BC
=> t/giác AMC cân tại M => ˆMAC=ˆCMAC^=C^
Ta có: ˆB+ˆC=900B^+C^=900 (phụ nhau)
ˆC+ˆHAC=900C^+HAC^=900 (phụ nhau)
=> ˆB=ˆHACB^=HAC^ hay ˆB=ˆOADB^=OAD^ (2)
Từ (1) và (2) => ˆODA=ˆBODA^=B^
Gọi I là giao điểm của MA và ED
Xét t/giác IAD có: ˆIAD+ˆIDA+ˆAID=1800IAD^+IDA^+AID^=1800 (tổng 3 góc của 1 t/giác)
=> ˆAID=1800−(IAD+ˆIDA)AID^=1800−(IAD+IDA^)
hay ˆAID=1800−(ˆB+ˆC)=1800−900=900AID^=1800−(B^+C^)=1800−900=900
=> AM⊥DEAM⊥DE(Đpcm)
c) (thiếu đề)