GIẢI GIÚP EM PT NÀY VỚI ẠA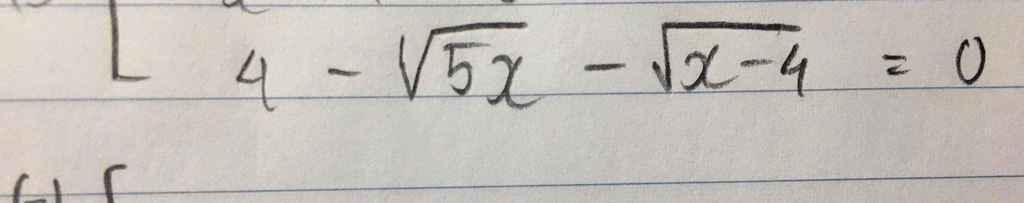
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PL
giúp em với ạa, bài này là bài tập không phải thi đâu ạa
0
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 7 2021
a.
\(\Leftrightarrow\dfrac{\sqrt{2}}{2}sin4x+\dfrac{\sqrt{2}}{2}cos4x=\dfrac{\sqrt{6}}{2}\)
\(\Leftrightarrow cos4x.cos\left(\dfrac{\pi}{4}\right)+sin4x.sin\left(\dfrac{\pi}{4}\right)=\dfrac{\sqrt{6}}{2}\)
\(\Leftrightarrow cos\left(4x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{6}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}4x-\dfrac{\pi}{4}=arccos\left(\dfrac{\sqrt{6}}{2}\right)+k2\pi\\4x-\dfrac{\pi}{4}=-arccos\left(\dfrac{\sqrt{6}}{2}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{16}+\dfrac{1}{4}arccos\left(\dfrac{\sqrt{6}}{2}\right)+\dfrac{k\pi}{4}\\x=\dfrac{\pi}{16}-\dfrac{1}{4}arccos\left(\dfrac{\sqrt{6}}{2}\right)+\dfrac{k\pi}{4}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 7 2021
b.
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sinx+\dfrac{1}{2}cosx=\dfrac{\sqrt{3}}{6}\)
\(\Leftrightarrow cosx.cos\left(\dfrac{\pi}{3}\right)+sinx.sin\left(\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{6}\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{6}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{3}=arccos\left(\dfrac{\sqrt{3}}{6}\right)+k2\pi\\x-\dfrac{\pi}{3}=-arccos\left(\dfrac{\sqrt{3}}{6}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+arccos\left(\dfrac{\sqrt{3}}{6}\right)+k2\pi\\x=\dfrac{\pi}{3}-arrcos\left(\dfrac{\sqrt{3}}{6}\right)+k2\pi\end{matrix}\right.\)
LN
mn giúp em câu này với ạa
0
NB
1
27 tháng 12 2023
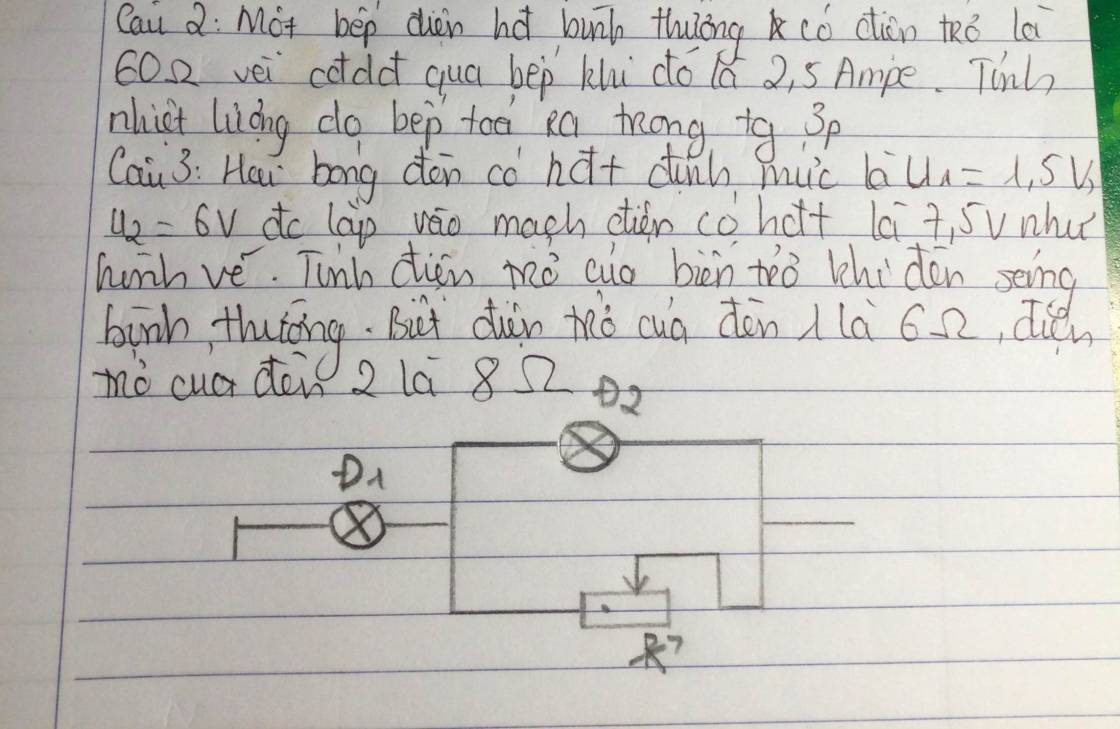
Câu 2.
Nhiệt lượng bếp tỏa ra trong thời gian \(t=3min=180s\) là:
\(Q=UIt=RI^2t=60\cdot2,5^2\cdot180=675000J\)
Câu 3.
\(I_{Đ1}=\dfrac{U_{Đ1}}{R_{Đ1}}=\dfrac{6}{6}=1A\)
\(I_{Đ2}=\dfrac{U_{Đ2}}{R_{Đ2}}=\dfrac{1,5}{8}=\dfrac{3}{16}A\)
\(I_b=I_{Đ1}-I_{Đ2}=1-\dfrac{3}{16}=\dfrac{13}{16}A\)
\(R_b=\dfrac{U_b}{I_b}=\dfrac{1,5}{\dfrac{13}{16}}=\dfrac{24}{13}\Omega\)
5 tháng 11 2021
bài 1:
\(\left\{{}\begin{matrix}x+y=57\\4x-2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+4y=228\\4x-2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6y=234\\x+y=57\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=39\\x=18\end{matrix}\right.\)
M
9 tháng 4 2022
c,\(\dfrac{5-x}{2}-\dfrac{3x+4}{3}=\dfrac{1}{4}\)
⇔\(\dfrac{5-x}{2}+\dfrac{-3x-4}{3}=\dfrac{1}{4}\)
⇔\(\dfrac{6\left(5-x\right)}{12}+\dfrac{4\left(-3x-4\right)}{12}=\dfrac{3}{12}\)
⇔6(5-x)+4(-3x-4)=3
⇔ 30-6x-12x-16=3
⇔ 30-16-3=12x+6x
⇔ 11=18x
⇔ x=\(\dfrac{11}{18}\)
Vậy S=\(\left\{\dfrac{11}{18}\right\}\)
d)x2-5x=9(x-5)
⇔x(x-5)=9(x-5)
⇔x(x-5)-9(x-5)=0
⇔(x-9)(x-5)=0
⇔\(\left\{{}\begin{matrix}x-9=0\Leftrightarrow x=9\\x-5=0\Leftrightarrow x=5\end{matrix}\right.\)
Vậy S=\(\left\{5;9\right\}\)
5 tháng 1 2022
a: =>x=y+11
xy=60
=>y(y+11)=60
\(\Leftrightarrow y^2+15y-4y-60=0\)
=>(y+15)(y-4)=0
hay \(y\in\left\{-15;4\right\}\)
15 tháng 6 2021
\(2sin^2x+5sinx-3=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx+3\right)=0\)
mà \(sinx\ge-1\Rightarrow sinx+3\ge2>0\)
\(\Rightarrow2sinx=1\Leftrightarrow sinx=\dfrac{1}{2}\)
\(\Leftrightarrow\)\(\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)(\(k\)\(\in\)\(Z\))
Ý D
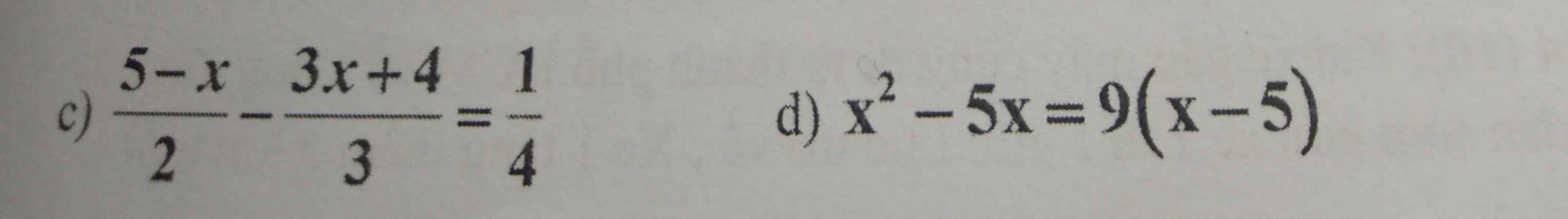
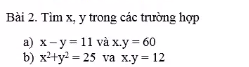
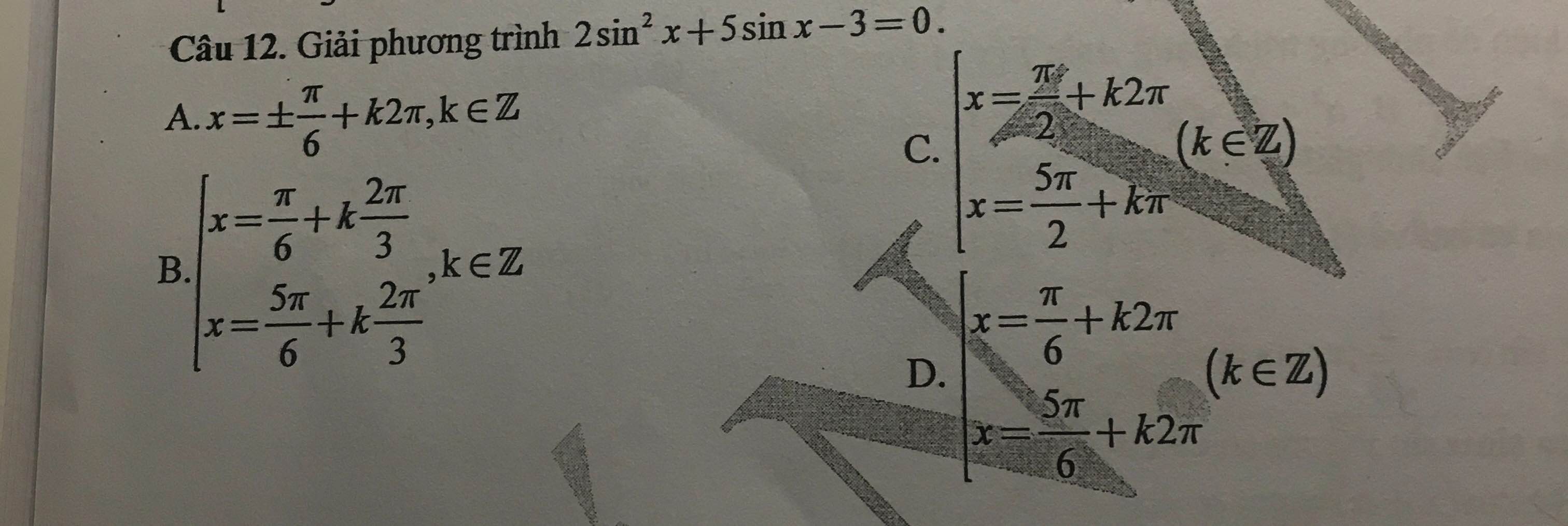
ĐKXĐ:\(x\ge4\)
\(4-\sqrt{5x}-\sqrt{x-4}=0\\ \Leftrightarrow4-\sqrt{5x}=\sqrt{x-4}\left(x\le\dfrac{16}{5}\right)\)
Vì \(x\ge4\) mà \(x\le\dfrac{16}{5}\) (vô lí)
\(\Rightarrow\) pt vô nghiệm