chứng tỏ rằng ax(a+3)-ax(a-4)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
5 tháng 12 2019
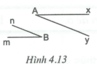
Gọi C là giao điểm của hai đường thẳng Ay và Bm.
Ta có Ax // Bm nên A ^ = A C m ^ (cặp góc so le trong).
Mặt khác A ^ = A C m ^ nên A C m ^ = m B n ^ = A ^ .
Do đó Ay // Bn (vì có cặp góc đồng vị bằng nhau)
CM
8 tháng 6 2017
Ở trong góc AOB vẽ tia O t / / A x . Khi đó A O t ^ = A ^ = a ° (cặp góc so le trong).
Suy ra B O t ^ = b ° . Vậy B O t ^ = B ^ = b ° .
Do đó By // Ot (vì có cặp góc so le trong bằng nhau).
Vậy Ax // By (vì cùng song song với Ot)
22 tháng 8 2016
\(\widehat{BAC}=180^o-\left(\widehat{B}+\widehat{C}\right)=180^o-80^o=100^o\)
\(\widehat{yAc}=180^o-100^o=80^o\)
Mà tia Ax là tia phân giạc góc ngoài của A
\(\Rightarrow\widehat{yAx}=\widehat{xAC}=\frac{\widehat{yAc}}{2}=\frac{80^o}{2}=40^o\)
Ở vị trí so le trong => Ax//BC
CM
1 tháng 1 2018
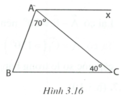
Tia AC nằm giữa hai tia AB và Ax nên B A C ^ + C A x ^ = B A x ^
⇒ C A x ^ = 110 ° − 70 ° = 40 ° .
Do đó C A x ^ = C ^ = 40 ° .
Suy ra Ax // BC vì có cặp góc so le trong bằng nhau
15 tháng 10 2015
Tam giác ABC có: góc B +góc C + góc BAC = 180o => 40o + 40o + BAC = 180o => góc BAC = 180o - 80o = 100o
=> góc BAy = 180o - BAC = 180o - 100o = 80o (do BAy là góc ngoài tam giác )
=> góc xAB = yAB/2 = 80o/2 = 40o (do Ax là p/g của góc yAB)
=> góc xAB = ABC (= 40o) Mà hai góc này ở vị trí SLT => Ax // BC