K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KV
30 tháng 8 2023
a) Vẽ tia By' là tia đối của tia By
Ta có:
∠ABy' + ∠ABy = 180⁰ (kề bù)
⇒ ∠ABy' = 180⁰ - ∠ABy
= 180⁰ - 135⁰
= 45⁰
⇒ ∠ABy' = ∠BAx = 45⁰
Mà ∠ABy' và ∠BAx là hai góc so le trong
⇒ By // Ax
b) Ta có:
∠CBy' = ∠ABC - ∠ABy'
= 75⁰ - 45⁰
= 30⁰
⇒ ∠CBy' = ∠BCz = 30⁰
Mà ∠CBy' và ∠BCz là hai góc so le trong
⇒ By // Cz
NQ
1
HD
17 tháng 9 2017
a)ta có xAB=ABy=90độ
vì xAB và ABy là 2 góc ở vị trí sole trong so với 2 dường thẳng Ax và By
=>Ax//By(2 góc sole trong bằng nhau)
b)ta có ABC=ABy+yBC
=>120=90+yBC
=>yBC=120-90=30
=>yBC=zCB=30
vì yBC và zCB là 2 góc ở vị trí đồng vị so với 2 đường thẳng By và Cz
=>By//Cz (2 góc đồng vị bằng nhau)
vậy a)Ax//By
b)By//Cz
CA
6 tháng 10
*Kẻ By’ là tia đối của tia By => ABy kề bù với ABy’
=> ABy + ABy’ = 180
=> 120 + ABy’ = 180
=> ABy’ = 60
Ta có mAx = 60 =ABy’ , mà mAx và ABy’ ở vị trí đồng vị => Ax // By (1)
*Ta có yBC + CBA + ABy = 360
=> yBC + 90 + 120 = 360
=> yBC = 150
Ta có BCz = 150 = yBC, mà 2 góc này ở vị trí so le trong => By // Cz (2)
Từ (1), (2) => đpcm
G
21 tháng 12 2017
Ta có: \(x+y+z=\left(by+cz\right)+\left(ax+cz\right)+\left(ax+by\right)=2\left(ax+by+cz\right)\)
=> \(x+y+z=2\left(ax+by+cz\right)=2\left[\left(ax+by\right)+cz\right]=2\left[z+cz\right]=2\left(1+c\right)z\)
=> \(\frac{1}{1+c}=\frac{2z}{x+y+z}\) (1)
Tượng tự:
\(\frac{1}{1+a}=\frac{2x}{x+y+z}\) (2)
\(\frac{1}{1+b}=\frac{2y}{x+y+z}\) (3)
Cộng các vế của (1), (2), (3) ta có:
\(\frac{1}{1+a}+\frac{1}{1+b}+\frac{1}{1+c}=\frac{2\left(x+y+z\right)}{x+y+z}=2\) (ĐPCM)
10 tháng 5 2020
Ta có x+y=ax+by+2cz=z+2cz
=> x+y-z=2cz
=> \(c=\frac{x+y-z}{2z}\Rightarrow c+1=\frac{x+y-z}{2z}+1=\frac{x+y+z}{2z}\)
\(\Rightarrow\frac{1}{c+1}=\frac{2z}{x+y+z}\left(1\right)\)
\(y+z=2ax+by+cz\Rightarrow y+z-x=2ax\Rightarrow a=\frac{y+z-x}{2x}\Rightarrow a+1=\frac{x+y+z}{2x}\)
\(\Rightarrow\frac{1}{a+1}=\frac{2x}{x+y+z}\left(2\right)\)
\(z+x=2by+ax+cz=2by+y\Rightarrow z+x-y=2by\)
\(\Rightarrow b=\frac{z+x-y}{2y}\Rightarrow b+1=\frac{z+x-y}{2y}+1=\frac{x+y+z}{2y}\)
\(\Rightarrow\frac{1}{b+1}=\frac{2y}{x+y+z}\left(3\right)\)
Cộng từng vế của (1)(2)(3) ta có
\(\frac{1}{a+1}+\frac{1}{b+1}+\frac{1}{c+1}=\frac{2x}{x+y+z}+\frac{2y}{x+y+z}+\frac{2z}{x+y+z}=\frac{2\left(x+y+z\right)}{x+y+z}=2\)
PT
1
CM
15 tháng 6 2018
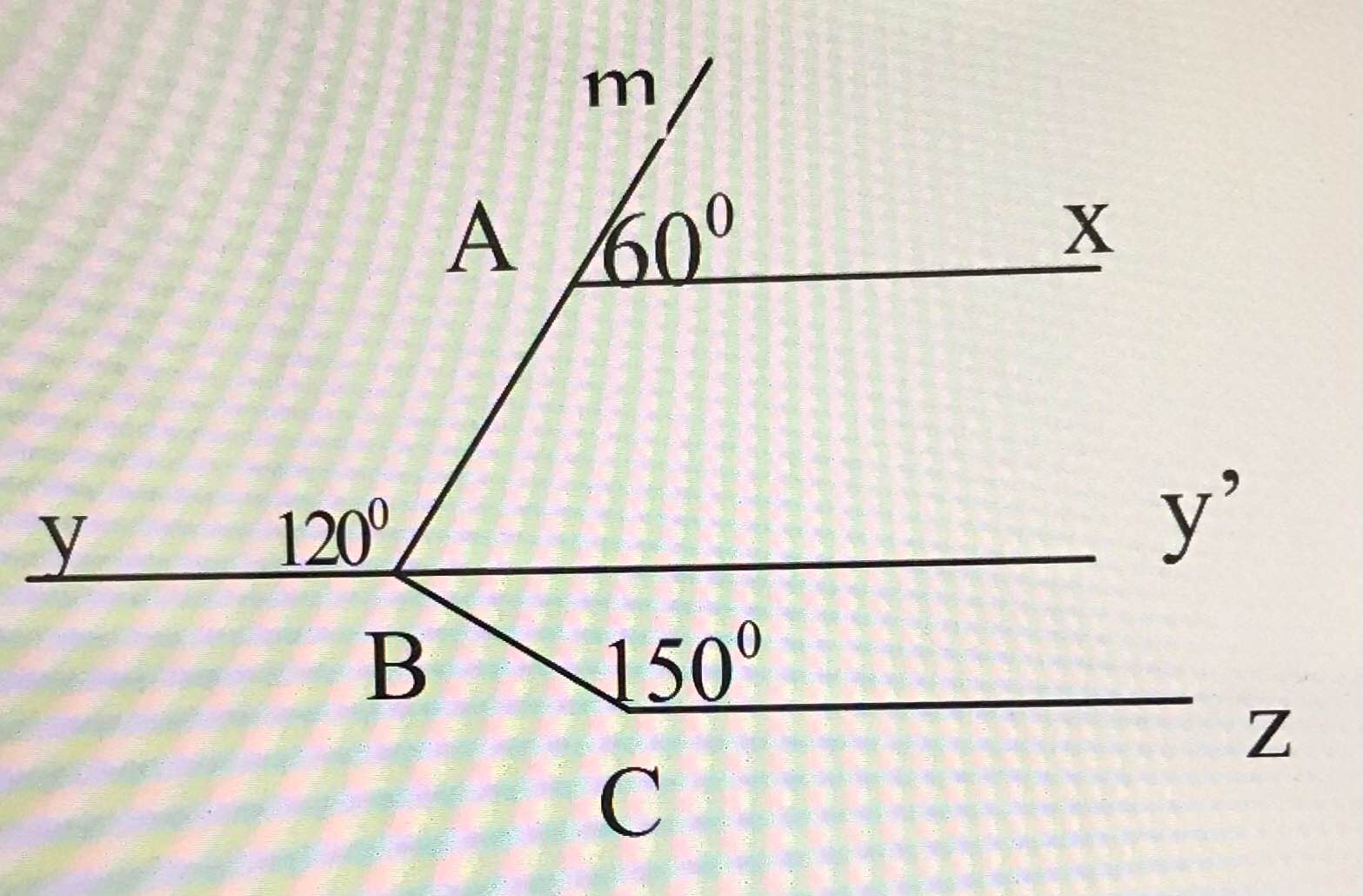
a) Ta có tAx ^ + xAB ^ = 180 ∘ (hai góc kề bù) mà tAx ^ = 60 ∘
⇒ xAB ^ = 180 ∘ − 60 ∘ = 120 ∘
Mặt khác ABy ^ = 120 ∘
⇒ xAB ^ = ABy ^ mà hai góc này ở vị trí so le trong
⇒ Ax // By
b)
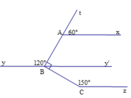
Kẻ tia By' là tia đối của tia By
Ta có: ABy ^ + ABy' ^ = 180 ∘ (hai góc kề bù) mà ABy ^ = 120 ∘
⇒ ABy' ^ = 180 ∘ − 120 ∘ = 60 ∘
Mặt khác ABC ^ = 90 ∘ hay ABy' ^ + y'BC ^ = 90 ∘
⇒ y'BC ^ = 90 ∘ − 60 ∘ = 30 ∘
Ta có y'BC ^ + CBy ^ = 180 ∘ (hai góc kề bù)
⇒ CBy ^ = 180 ∘ − 30 ∘ = 150 ∘
Ta lại có BCz ^ = 150 ∘
⇒ BCz ^ = CBy ^ mà hai góc này ở vị trí so le trong
⇒ By // Cz
