GIÚP EM VỚI ẠAAAAA
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




bài 1:
a, Mỗi khi trời đổ mưa to thì em lại cùng đám bạn quây quầy bên bếp lửa.
b, Nếu em chăm chỉ học bài thì em sẽ đạt kết quả cao
c, Lan được cô khen nhờ Lan vẫn chăm chỉ làm hết bài tập về nhà
d, Thấy mẹ đang bận nấu cơm ở trong bếp nên em liền phụ mẹ tưới cây
Bài 2:
a, Còn
b, Nên
c,Vì... nên...
d,Tuy...nhưng...
e, Do... nên ( chắc vậy)

45. I know how to use this machine, I can help you.
46. excited about the journey.
47. Peter is the best student in my class who can solve this difficult problem.
48. very good at typing.

Câu 2:
=>x=1-y và m(1-y)-y=2m
=>x=1-y và m-my-y=2m
=>x=1-y và y(-m-1)=m
=>x=1-y và y=-m/m+1
=>x=1+m/m+1=(m+2)/m+1 và y=-m/m+1
Để x,y nguyên thì m+1+1 chia hết cho m+1 và -m-1+1 chia hết cho m+1
=>\(m+1\in\left\{1;-1\right\}\)
mà m<>0
nên m=-2





 giúp em vs ạaaaaa
giúp em vs ạaaaaa

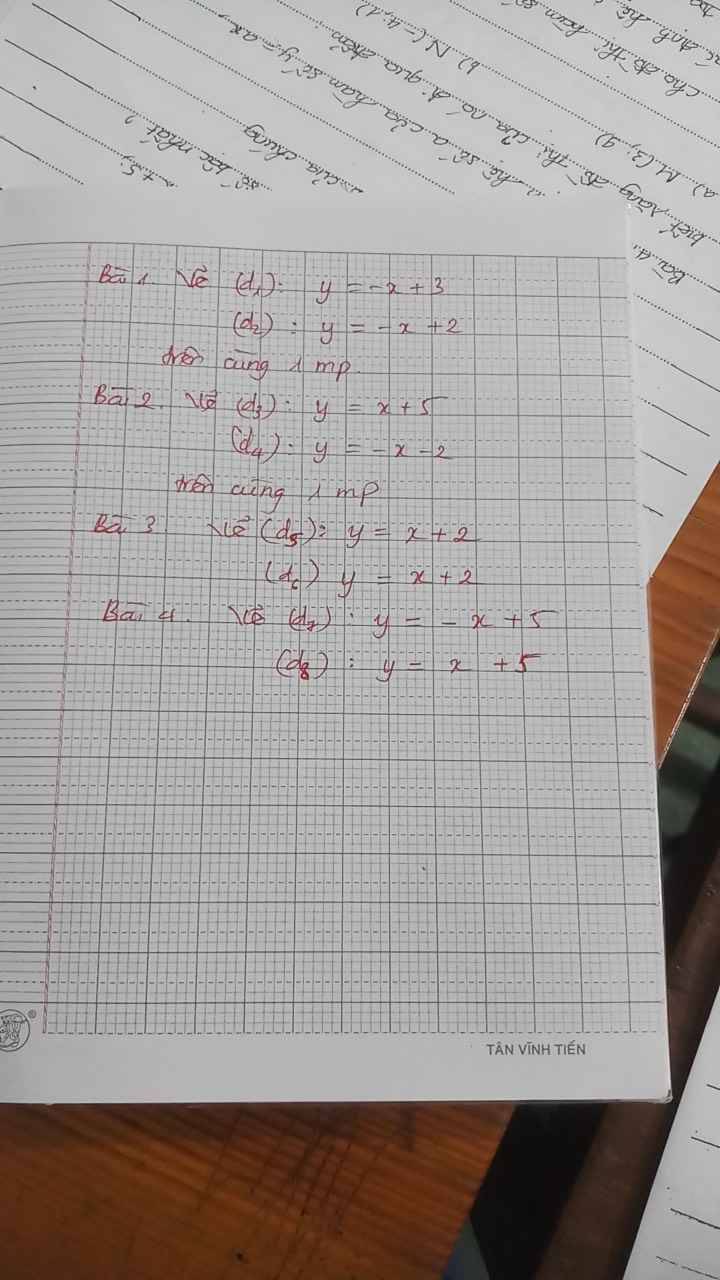
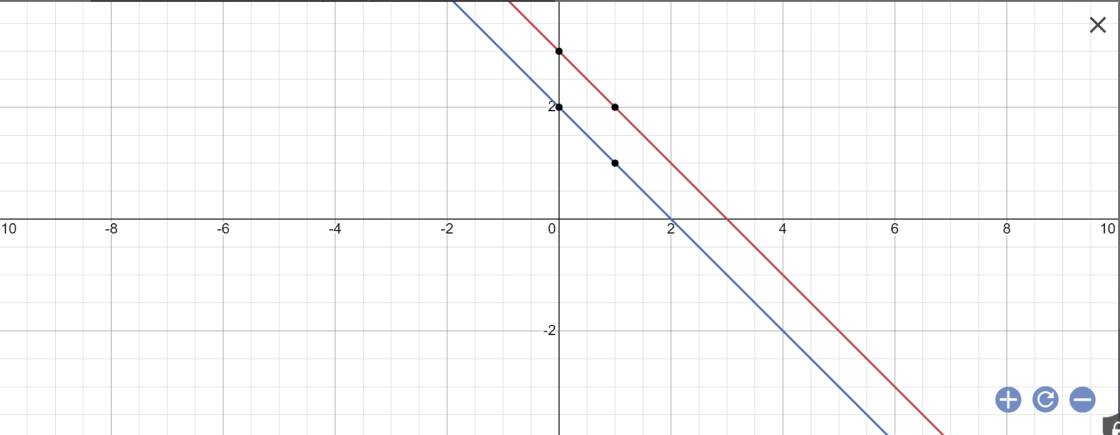
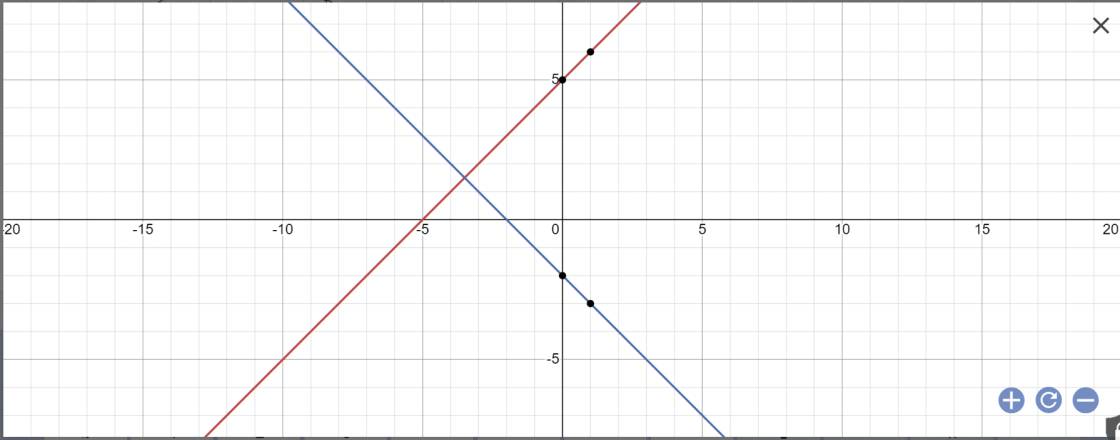
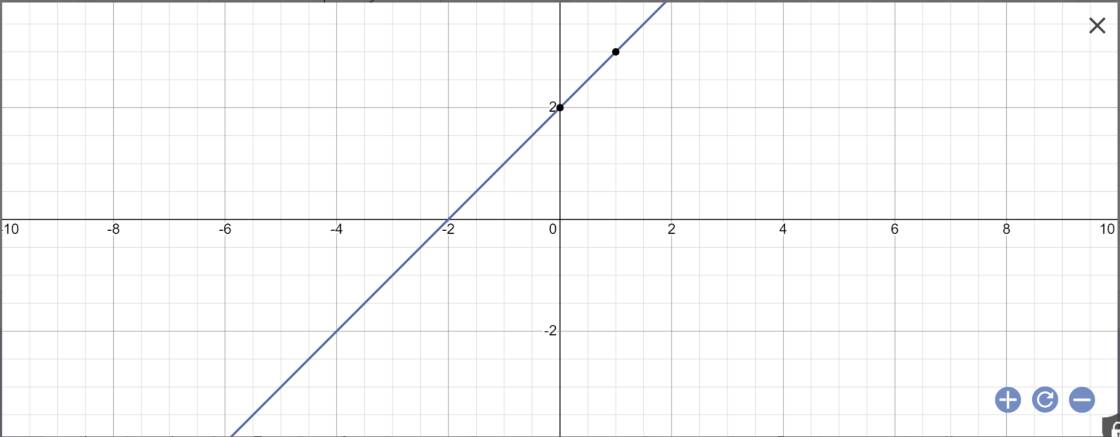
 giúp mình câu 2 với ạaaaaa
giúp mình câu 2 với ạaaaaa
Ta có: \(x^2-3x+2=\left(1-x\right)\sqrt{3x-2}\) \(\left(x\ge\dfrac{2}{3}\right)\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)-\left(1-x\right)\sqrt{3x-2}=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2+\sqrt{3x-2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-2+\sqrt{3x-2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(TM\right)\\\sqrt{3x-2}=2-x\left(1\right)\end{matrix}\right.\)
Xét (1) ta có: \(\left\{{}\begin{matrix}2-x\ge0\\3x-2=4-4x+x^2\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}2\ge x\\x^2-7x+6=0\end{matrix}\right.\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x\le2\\\left[{}\begin{matrix}x=6\left(KTM\right)\\x=1\left(TM\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy nghiệm của phương trình là x=1
ĐKXĐ : x \(\ge\dfrac{2}{3}\)
Ta có \(\left(x-1\right)\left(x-2\right)=\sqrt{3x-2}\left(1-x\right)\)
<=> \(\left(x-1\right)\left(x-2+\sqrt{3x-2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\\sqrt{3x-2}=2-x\end{matrix}\right.\)
Khi x - 1 = 0 <=> x = 1 (tm)
Khi \(\sqrt{3x-2}=2-x\)
<=> \(\left\{{}\begin{matrix}3x-2=x^2-4x+4\\\dfrac{2}{3}\le x\le2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-7x+6=0\\\dfrac{2}{3}\le x\le2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(x-6\right)=0\\\dfrac{2}{3}\le x\le2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=6\end{matrix}\right.\\\dfrac{2}{3}\le x\le2\end{matrix}\right.\Leftrightarrow x=1\)
Vậy phương trình 1 nghiêm \(x=1\)