Mọi người có thể giúp mình ko ạ . Mình xin cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NL
1
21 tháng 10 2021
\(d,ĐK:x\ge1\\ PT\Leftrightarrow\sqrt{x-1}=2+\sqrt{x+1}\\ \Leftrightarrow x-1=2+x+1+4\sqrt{x+1}\\ \Leftrightarrow4\sqrt{x+1}=-4\Leftrightarrow x\in\varnothing\left(4\sqrt{x+1}\ge0\right)\\ g,ĐK:x\ge\dfrac{1}{2}\\ PT\Leftrightarrow x+\sqrt{2x-1}+x-\sqrt{2x-1}+2\sqrt{\left(x+\sqrt{2x-1}\right)\left(x-\sqrt{2x-1}\right)}=2\\ \Leftrightarrow2x+2\sqrt{x^2-2x+1}=2\\ \Leftrightarrow\sqrt{\left(x-1\right)^2}=\dfrac{2-2x}{2}=1-x\\ \Leftrightarrow\left|x-1\right|=1-x\\ \Leftrightarrow\left[{}\begin{matrix}x-1=1-x\left(x\ge1\right)\\x-1=x-1\left(x< 1\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x\in R\end{matrix}\right.\)
NA
1
HL
1
TP
9 tháng 12 2021
\(a.Tacó:\left\{{}\begin{matrix}2Z+N=60\\2Z-N=4\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}Z=16\\N=28\end{matrix}\right.\\ Z=16\Rightarrow Cấuhìnhe:1s^22s^22p^63s^23p^4\)
b. Từ cấu hình e ta thấy:
Số lớp X : 3
Số e ở phân lớp năng lượng cao nhất là 4
c.\(X+2e\rightarrow X^{2-}\)
\(\Rightarrow CấuhìnheX^{2-}:1s^22s^22p^63s^23p^6\)
HT
1
19 tháng 8 2021
PTHH: \(Al_2O_3+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2O\)
Ta có: \(\left\{{}\begin{matrix}m_{H_2SO_4}=588\cdot5\%=29,4\left(g\right)\Rightarrow n_{H_2SO_4}=\dfrac{29,4}{98}=0,3\left(mol\right)\\n_{Al_2O_3}=\dfrac{20,4}{102}=0,2\left(mol\right)\end{matrix}\right.\)
Xét tỉ lệ: \(\dfrac{0,2}{1}>\dfrac{0,3}{3}\) \(\Rightarrow\) Al2O3 còn dư
\(\Rightarrow n_{Al_2\left(SO_4\right)_3}=0,1\left(mol\right)=n_{Al_2O_3\left(dư\right)}\)
\(\Rightarrow C\%_{Al_2\left(SO_4\right)_3}=\dfrac{0,1\cdot342}{20,4+588-0,1\cdot102}\cdot100\%\approx5,72\%\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 1 2022
Hàm bậc 2 có \(\left\{{}\begin{matrix}a=1>0\\-\dfrac{b}{2a}=6-m\end{matrix}\right.\) nên nghịch biến trên khoảng \(\left(-\infty;6-m\right)\)
Hàm nghịch biến trên khoảng đã cho khi:
\(6-m\ge2\Rightarrow m\le4\)
\(\Rightarrow\) Có 4 giá trị nguyên dương của m
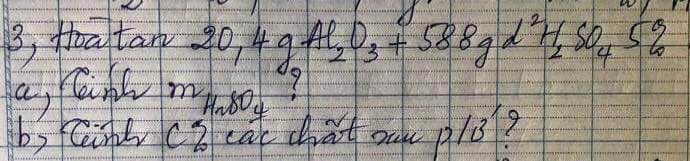
\(\Leftrightarrow\left(x+3\right)^2\cdot\left(x-3\right)^2-6\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left[\left(x^2-9\right)\left(x-3\right)-6\right]=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^3-3x^2-9x+21\right)=0\)
=>x+3=0
hay x=-3
\(\Leftrightarrow\left(x+3\right)^2\left(x-3\right)^2=6\left(x+3\right)\)
\(\Leftrightarrow\left(x+3\right)\left[\left(x+3\right)\left(x-3\right)^2-6\right]=0\)
Vì \(\left[\left(x+3\right)\left(x-3\right)^2-6\right]\ne0\)
\(\Rightarrow x+3=0\)
\(\Rightarrow x=-3\)