
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=x^2-4xy+4y^2+2x-4y+1+y^2+2y+1+2008\)
\(A=\left(x-2y\right)^2+2\left(x-2y\right)+1+\left(y+1\right)^2+2008\)
\(A=\left(x-2y+1\right)^2+\left(y+1\right)^2+2008\ge2008\)
\(\Rightarrow A_{min}=2008\Leftrightarrow\left\{{}\begin{matrix}x-2y+1=0\\y+1=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-1\end{matrix}\right.\)

a: \(=\dfrac{x+2}{x+2}=1\)
b: \(=\dfrac{2x+6}{x+3}=2\)


ĐKXĐ : \(x\ne\pm2\)
Ta có : \(A=\left(\dfrac{\left(x+1\right)\left(x+2\right)+x\left(x-2\right)+2x^2+3}{x^2-4}\right):\left(\dfrac{x+2-x+3}{x+2}\right)\)
\(=\left(\dfrac{4x^2+x+5}{x^2-4}\right):\left(\dfrac{5}{x+2}\right)=\dfrac{\left(4x^2+x+5\right)\left(x+2\right)}{5\left(x+2\right)\left(x-2\right)}=\dfrac{4x^2+x+5}{5x-10}\)
\(=\dfrac{4x+9}{5}+\dfrac{23}{5x-10}\)
- Để A nhận giá trị nguyên :
\(5\left(x-2\right)\inƯ_{\left(23\right)}=\left\{1;-1;23;-23\right\}\)
\(\Rightarrow x\in\left\{\dfrac{11}{5};\dfrac{9}{5};\dfrac{33}{5};-\dfrac{13}{5}\right\}\)
=> Không tồn tại x nguyên để A nguyên .


tr 10h à còn sớm
P=x2 - 2x + 5
=x2-2x+1+4
=(x-1)2+4
Ta thấy:\(\left(x-1\right)^2+4\ge0+4=4\)
Dấu = khi x=1
Vậy Pmin=4 <=>x=1
Q= 2x2 -6x
\(=2x^2-6x+\frac{9}{2}-\frac{9}{2}\)
\(=2\left(x^2-3x+\frac{9}{4}\right)-\frac{9}{2}\)
\(=2\left(x-\frac{3}{2}\right)\left(x-\frac{3}{2}\right)-\frac{9}{2}\)
\(=2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}\)
Ta thấy:\(2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}\ge0-\frac{9}{2}=-\frac{9}{2}\)
Dấu = khi x=3/2
Vậy Qmin=-9/2 <=>x=3/2
P = x2 - 2x + 5 = x(x - 2) + 5 nhỏ nhất khi x(x - 2) nhỏ nhất .
Xét x(x - 2) < 0 (để nhỏ nhất) thì x và x - 2 khác dấu mà x > x - 2 nên x > 0 > x - 2 => 2 > x > 0 => x = 1 => x(x - 2) = -1
Vậy P min = -1 + 5 = 4
Q = 2x2 - 6x = 2x(x - 3) nhỏ nhất khi x(x - 3) nhỏ nhất
Xét x(x - 3) < 0 (để nhỏ nhất) thì x và x - 3 khác dấu mà x > x - 3 nên x > 0 > x - 3 => 3 > x > 0 => x = 1;2
Ta thấy x(x - 3) = -2 tại x = 1 và x = 2 nên [x(x - 3)]min = -2 => Qmin = -2.2 = -4

a, ĐKXĐ:\(2x^3-2x^2\ne0\Rightarrow2x^2\left(x-1\right)\ne0\Rightarrow\left\{{}\begin{matrix}2x^2\ne0\\x-1\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ne0\\x\ne1\end{matrix}\right.\)
b, \(A=\dfrac{5x^2-5x}{2x^3-2x^2}\)
\(\Rightarrow A=\dfrac{5x\left(x-1\right)}{2x^2\left(x-1\right)}\)
\(\Rightarrow A=\dfrac{5}{2x}\)
Để A=1\(\Rightarrow\dfrac{5}{2x}=1\)
\(\Rightarrow2x=5\\ \Rightarrow x=\dfrac{5}{2}\)
a, đk \(2x^2\left(x-1\right)\ne0\Leftrightarrow x\ne0;x\ne1\)
b, \(A=\dfrac{5x\left(x-1\right)}{2x^2\left(x-1\right)}=\dfrac{5}{2x}=1\Rightarrow5=2x\Leftrightarrow x=\dfrac{5}{2}\left(tm\right)\)

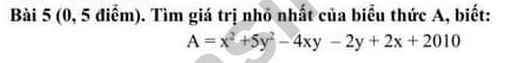





\(\Leftrightarrow\left(x+3\right)^2\cdot\left(x-3\right)^2-6\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left[\left(x^2-9\right)\left(x-3\right)-6\right]=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^3-3x^2-9x+21\right)=0\)
=>x+3=0
hay x=-3
\(\Leftrightarrow\left(x+3\right)^2\left(x-3\right)^2=6\left(x+3\right)\)
\(\Leftrightarrow\left(x+3\right)\left[\left(x+3\right)\left(x-3\right)^2-6\right]=0\)
Vì \(\left[\left(x+3\right)\left(x-3\right)^2-6\right]\ne0\)
\(\Rightarrow x+3=0\)
\(\Rightarrow x=-3\)