giải hộ mình bài 3 với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
Thay x=2, y=3 vào M ta có:
\(M=5xy-10+2y=5.3.2-10+3.3=30-10+9=29\)
Bài 3:
\(a,A=\left(2x^3y\right)\left(-3xy\right)=-6x^4y^2\)
Hệ số: -6
Bậc:6
\(b,B=\left(-\dfrac{1}{16}x^2y^2\right)\left(4x^3\right)\left(8xyz\right)=-2x^6y^3z\)
Hệ số: -2
Bậc:10
\(c,\dfrac{-3}{25}x\left(\dfrac{1}{3}x^3y\right)^2\left(\dfrac{5}{2}y^3\right)^2=\dfrac{-3}{25}x\left(\dfrac{1}{9}x^6y^2\right)\left(\dfrac{25}{4}y^6\right)=-\dfrac{1}{12}x^7y^8\)
Hệ số: -1/12
Bậc:15

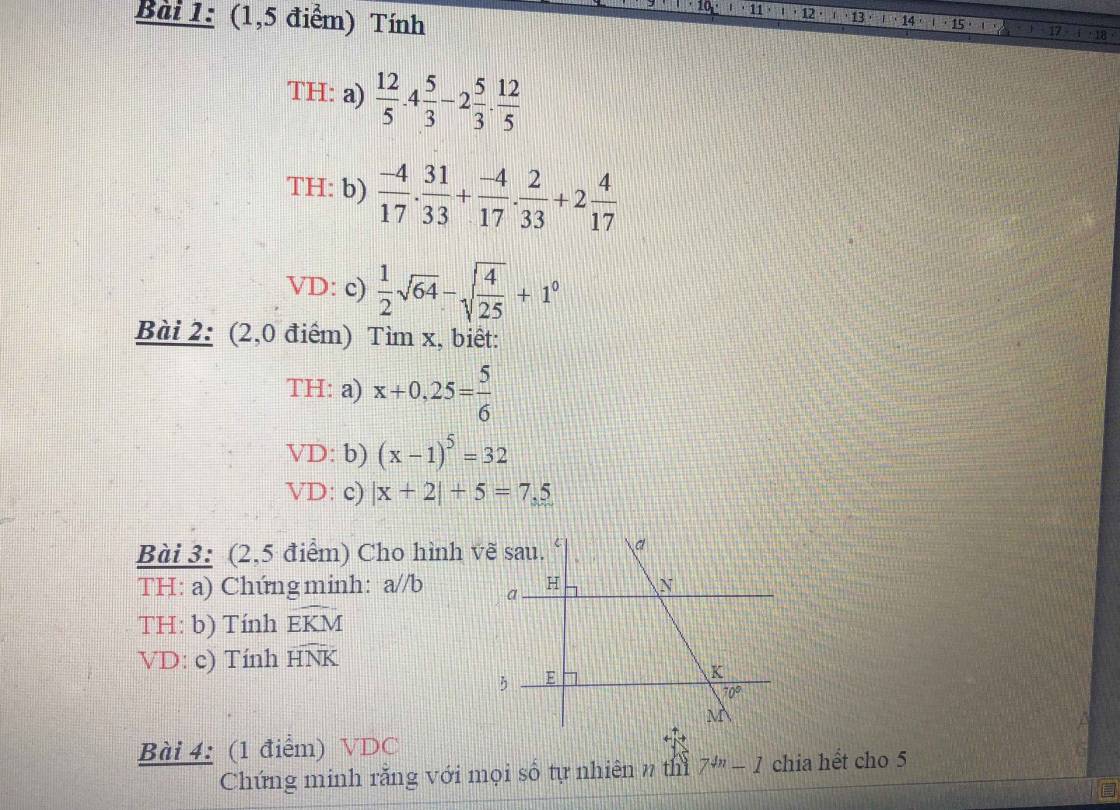
3:
a: a\(\perp\)HE
b\(\perp\)HE
Do đó: a//b
b:
Gọi Kc là tia đối của tia Kb
=>\(\widehat{cKM}=70^0\)
\(\widehat{EKM}+\widehat{MKc}=180^0\)(hai góc kề bù)
=>\(\widehat{EKM}+70^0=180^0\)
=>\(\widehat{EKM}=110^0\)
c: HN//EK
=>\(\widehat{HNK}=\widehat{EKM}\)(hai góc đồng vị)
mà \(\widehat{EKM}=110^0\)
nên \(\widehat{HNK}=110^0\)



a) Phương trình hoành độ giao điểm là:
\(x^2=\left(m+2\right)x-2m\)
\(\Leftrightarrow x^2-\left(m+2\right)x+2m=0\)
\(\Delta=\left(m+2\right)^2-8m=m^2+4m+4-8m=m^2-4m+4=\left(m-2\right)^2\)
Để (d) và (P) cắt nhau tại hai điểm phân biệt thì \(\Delta>0\)
\(\Leftrightarrow\left(m-2\right)^2>0\)
mà \(\left(m-2\right)^2\ge0\)
nên \(m-2\ne0\)
hay \(m\ne2\)
Vậy: Để (d) và (P) cắt nhau tại hai điểm phân biệt thì \(m\ne2\)


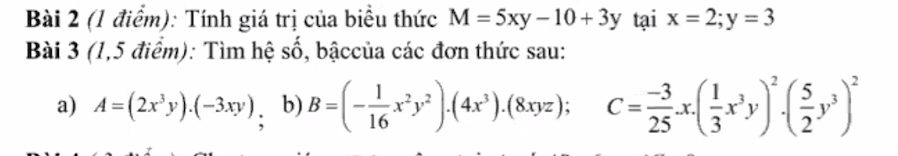
 giải hộ mình bài 3 với ạ
giải hộ mình bài 3 với ạ 

quay ngược cái ảnh lại chứ gãy cổ òi
Ủ bạn có phần quay sẵn rồi mà???