Tìm giá trị nhỏ nhất của biểu thức:
P = x2 + 5y2 + 2xy - 4x - 8y + 2015
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AP
4
LV
23 tháng 1 2017
Giải :(x2+2xy+y2)+y2-6x-8y+2024=(x+y)2-2(x+y)3+y2-2y+2024
=(x+y-3)2+(y2-2y+1)+2014=(x+y-3)2+(y-1)2+2014 >=2014
vì (x+y-3)2;(y-1)2>=0 với mọi x;y
nên Pmin=2014khi y=1;x=2
9 tháng 7 2021
Bài 3:
a) Ta có: \(A=25x^2-20x+7\)
\(=\left(5x\right)^2-2\cdot5x\cdot2+4+3\)
\(=\left(5x-2\right)^2+3>0\forall x\)(đpcm)
d) Ta có: \(D=x^2-2x+2\)
\(=x^2-2x+1+1\)
\(=\left(x-1\right)^2+1>0\forall x\)(đpcm)
9 tháng 7 2021
Bài 1:
a) Ta có: \(A=x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi x=1
b) Ta có: \(B=x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
6 tháng 10 2021
\(a,f\left(x\right)⋮g\left(x\right)\\ \Leftrightarrow\dfrac{-x^4+2x^2-3x+5}{x-1}\in Z\\ \Leftrightarrow\dfrac{-x^4+x^3-x^3+x^2+x^2-x-2x+2+3}{x-1}\in Z\\ \Leftrightarrow\dfrac{-x^3\left(x-1\right)-x^2\left(x-1\right)+x\left(x-1\right)-2\left(x-1\right)+3}{x-1}\in Z\\ \Leftrightarrow-x^3-x^2+x-2+\dfrac{3}{x-1}\in Z\\ \Leftrightarrow3⋮x-1\\ \Leftrightarrow x-1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Leftrightarrow x\in\left\{-2;0;2;4\right\}\\ Mà.x< 0\\ \Leftrightarrow x=-2\\ b,B=\left(x^2-2xy+y^2\right)+4\left(x-y\right)+4+4y^2-2024\\ B=\left(x-y\right)^2+4\left(x-y\right)+4+4y^2-2024\\ B=\left(x-y-2\right)^2+4y^2-2024\ge-2024\\ B_{min}=-2024\Leftrightarrow\left\{{}\begin{matrix}x=y+2\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
27 tháng 5 2023
Lời giải:
$P=(x^2+y^2+2xy)+y^2-6x-8y+2028$
$=(x+y)^2-6(x+y)+(y^2-2y)+2028$
$=(x+y)^2-6(x+y)+9+(y^2-2y+1)+2018$
$=(x+y-3)^2+(y-1)^2+2018\geq 0+0+2018=2018$
Vậy $P_{\min}=2018$
Giá trị này đạt tại $x+y-3=y-1=0$
$\Leftrightarrow y=1; x=2$
27 tháng 8 2021
`A=x^2-4x+y^2-8y+6`
`A=x^2-4x+4+y^2-8y+16-14`
`A=(x-2)^2+(y-4)^2-14`
VÌ `(x-2)^2+(y-4)^2>=0`
`=>(x-2)^2+(y-4)^2-14>=-14`
`=>A>=-14`
Dấu "=" xảy ra khi `x-2=0,y-4=0<=>{(x=2),(y=4):}`
AK
0
PT
1
CM
9 tháng 2 2017
Q = x 2 + 2 y 2 + 2 x y − 2 x − 6 y + 2015 = x 2 + 2 x y + y 2 − 2 x − 2 y + 1 + y 2 − 4 y + 4 + 2010 = x 2 + 2 x y + y 2 − 2 x + 2 y + 1 + y 2 − 4 y + 4 + 2010 = x + y 2 − 2 x + y + 1 + y 2 − 4 y + 4 + 2010 = x + y − 1 2 + y − 2 2 + 2010
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 5 2021
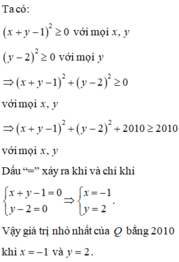
\(P=x^2-6x+9+2\)
\(P=\left(x-3\right)^2+2\)
Do \(\left(x-3\right)^2\ge0\) ;\(\forall x\)
\(\Rightarrow P\ge0+2\Rightarrow P\ge2\)
Vậy \(P_{min}=2\) khi \(x=3\)
\(P=\left(x^2+2xy+y^2\right)-4x-4y+4+\left(4y^2-4y+1\right)+2010\)
\(=\left(x+y\right)^2-4\left(x+y\right)+4+\left(2y-1\right)^2+2010\)
\(P=\left(x+y-2\right)^2+\left(2y-1\right)^2+2010\ge2010\) với mọi \(x,y\)
Dấu \("="\) xảy ra \(\Leftrightarrow\) \(\left(x+y-2\right)^2=0\) và \(\left(2y-1\right)^2=0\)
\(\Leftrightarrow\) \(x+y-2=0\) và \(2y-1=0\)
\(\Leftrightarrow\) \(x=2-y\) và \(y=\frac{1}{2}\)
\(\Leftrightarrow\) \(x=\frac{3}{2}\) và \(y=\frac{1}{2}\)
Vậy, \(P_{min}=2010\) \(\Leftrightarrow\) \(x=\frac{3}{2};\) và \(y=\frac{1}{2}\)