tìm m để hàm số \(y=\dfrac{2x+1}{x^2-2x+m-3}\) xác định
trên (âm vô cùng, -2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2022
Hàm xác định trên \(\left[2;3\right]\) khi và chỉ khi:
\(x^2-2x-m>0;\forall x\in\left[2;3\right]\)
\(\Rightarrow x^2-2x>m;\forall x\in\left[2;3\right]\)
\(\Rightarrow m< \min\limits_{\left[2;3\right]}\left(x^2-2x\right)\)
Xét hàm \(f\left(x\right)=x^2-2x\) trên \(\left[2;3\right]\)
\(-\dfrac{b}{2a}=1\notin\left[2;3\right]\)
\(f\left(2\right)=0\) ; \(f\left(3\right)=3\)
\(\Rightarrow\min\limits_{\left[2;3\right]}\left(x^2-2x\right)=0\)
\(\Rightarrow m< 0\)
14 tháng 7 2021
Bài 1:
a) Để hàm số y=(k-2)x+k+3 là hàm số bậc nhất thì \(k\ne2\)
b) Để hàm số y=(k-2)x+k+3 đồng biến trên R thì k-2>0
hay k>2
Bài 2:
Thay \(x=-\dfrac{1}{2}\) và \(y=\dfrac{2}{3}\) vào (D), ta được:
\(\left(2m-3\right)\cdot\dfrac{-1}{2}-\dfrac{1}{2}=\dfrac{2}{3}\)
\(\Leftrightarrow\left(2m-3\right)\cdot\dfrac{-1}{2}=\dfrac{2}{3}+\dfrac{1}{2}=\dfrac{7}{6}\)
\(\Leftrightarrow2m-3=\dfrac{7}{6}:\dfrac{-1}{2}=\dfrac{-7}{6}\cdot\dfrac{2}{1}=-\dfrac{14}{6}=-\dfrac{7}{3}\)
\(\Leftrightarrow2m=\dfrac{-7}{3}+3=\dfrac{-7}{3}+\dfrac{9}{3}=\dfrac{2}{3}\)
hay \(m=\dfrac{1}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 6 2021
\(y'=x^2-2\left(m-2\right)x+m^2-3m+2\)
a. Hàm đồng biến trên khoảng đã cho khi và chỉ khi:
\(y'\ge0\) ; \(\forall x>3\)
\(\Leftrightarrow x^2-2\left(m-2\right)x+m^2-3m+2\ge0\) ; \(\forall x>3\)
Ta có: \(\Delta'=\left(m-2\right)^2-\left(m^2-3m+2\right)=-m+2\)
TH1: \(\Delta'\le0\Leftrightarrow m\ge2\)
TH2: \(\left\{{}\begin{matrix}\Delta'>0\\x_1< x_2\le2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\\left(x_1-2\right)\left(x_2-2\right)\ge0\\\dfrac{x_1+x_2}{2}< 2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\x_1x_2-2\left(x_1+x_2\right)+4\ge0\\x_1+x_2< 4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m^2-3m+2-4\left(m-2\right)+4\ge0\\2\left(m-2\right)< 4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m^2-7m+4\ge0\\m< 4\end{matrix}\right.\) \(\Leftrightarrow m< 2\)
Kết hợp lại ta được hàm đồng biến trên \(\left(2;+\infty\right)\) với mọi m
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 6 2021
b.
Hàm số đồng biến trên khoảng đã cho khi và chỉ khi:
\(y'\ge0\) ; \(\forall x< 0\)
\(\Leftrightarrow x^2-2\left(m-2\right)x+m^2-3m+2\ge0\) ; \(\forall x< 0\)
TH1: \(\Delta'=-m+2\le0\Leftrightarrow m\ge2\)
TH2: \(\left\{{}\begin{matrix}\Delta'>0\\0\le x_1< x_2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 2\\x_1+x_2=2\left(m-2\right)>0\\x_1x_2=m^2-3m+2\ge0\end{matrix}\right.\) \(\Rightarrow\) ko tồn tại m thỏa mãn
Kết hợp lại ta được: \(m\ge2\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 6 2021
\(y'=3x^2-6mx+3\left(3m-4\right)=3\left[x^2-2mx+3m-4\right]\)
Xét \(f\left(x\right)=x^2-2mx+3m-4\)
\(\Delta'=m^2-3m+4=\left(m-\dfrac{3}{2}\right)^2+\dfrac{7}{4}>0\) ;\(\forall m\)
a. Để hàm số đồng biến trên khoảng đã cho
\(\Leftrightarrow x^2-2mx+3m-4\ge0\) ; \(\forall x\le1\)
\(\Leftrightarrow1\le x_1< x_2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x_1-1\right)\left(x_2-1\right)\ge0\\\dfrac{x_1+x_2}{2}>1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2-\left(x_1+x_2\right)+1\ge0\\x_1+x_2>2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3m-4-2m+1\ge0\\2m>2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ge3\\m>1\end{matrix}\right.\) \(\Rightarrow m\ge3\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 6 2021
b.
Để hàm đồng biến trên khoảng đã cho
\(\Leftrightarrow x^2-2mx+3m-4\ge0\) ; \(\forall x\ge2\)
\(\Leftrightarrow x_1< x_2\le2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x_1-2\right)\left(x_2-2\right)\ge0\\\dfrac{x_1+x_2}{2}< 2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2-2\left(x_1+x_2\right)+4\ge0\\x_1+x_2< 4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3m-4-4m+4\ge0\\2m< 4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\le0\\m< 2\end{matrix}\right.\) \(\Rightarrow m\le0\)
25 tháng 12 2023
Xét parabol \(\left(C_m\right):y=-2x^2-\left(2m-1\right)x+6-3m\), ta có \(\Delta=\left[-\left(2m-1\right)\right]^2-4\left(-2\right)\left(6+3m\right)=4m^2+20m+49\)
Gọi \(I_m\) là đỉnh của \(\left(C_m\right)\) thì \(I_m\left(\dfrac{-2m+1}{4};\dfrac{4m^2+20m+49}{8}\right)\)
Để hàm số đã cho nghịch biến trong khoảng \(\left(-2;+\infty\right)\) thì \(\dfrac{-2m+1}{4}=-2\Leftrightarrow m=\dfrac{9}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 7 2021
1.
Đồ thị hàm bậc 3 có 2 điểm cực trị nằm về 2 phía trục hoành khi và chỉ khi \(f\left(x\right)=0\) có 3 nghiệm phân biệt
\(\Leftrightarrow x^3+3x^2+mx+m-2=0\) có 3 nghiệm pb
\(\Leftrightarrow x^3+3x^2-2+m\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x-2\right)+m\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x+m-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2+2x+m-2=0\left(1\right)\end{matrix}\right.\)
Bài toán thỏa mãn khi (1) có 2 nghiệm pb khác -1
\(\Leftrightarrow\left\{{}\begin{matrix}1-2+m-2\ne0\\\Delta'=1-\left(m-2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow m< 3\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 7 2021
2.
Pt hoành độ giao điểm:
\(\dfrac{2x-2}{x+1}=2x+m\)
\(\Rightarrow2x-2=\left(2x+m\right)\left(x+1\right)\)
\(\Leftrightarrow2x^2+mx+m+2=0\) (1)
d cắt (C) tại 2 điểm pb \(\Rightarrow\) (1) có 2 nghiệm pb
\(\Rightarrow\Delta=m^2-8\left(m+2\right)>0\Rightarrow\left[{}\begin{matrix}m>4+4\sqrt{2}\\m< 4-4\sqrt{2}\end{matrix}\right.\)
Khi đó, theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=-\dfrac{m}{2}\\x_Ax_B=\dfrac{m+2}{2}\end{matrix}\right.\)
\(y_A=2x_A+m\) ; \(y_B=2x_B+m\)
\(\Rightarrow AB^2=\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2=5\)
\(\Leftrightarrow\left(x_A-x_B\right)^2+\left(2x_A-2x_B\right)^2=5\)
\(\Leftrightarrow\left(x_A-x_B\right)^2=1\)
\(\Leftrightarrow\left(x_A+x_B\right)^2-4x_Ax_B=1\)
\(\Leftrightarrow\left(-\dfrac{m}{2}\right)^2-4\left(\dfrac{m+2}{2}\right)=1\)
\(\Leftrightarrow m^2-8m-20=0\Rightarrow\left[{}\begin{matrix}m=10\\m=-2\end{matrix}\right.\)
Hàm xác định trên khoảng đã cho khi và chỉ khi:
\(x^2-2x+m-3=0\) vô nghiệm trên khoảng đã cho
\(\Leftrightarrow x^2-2x-3=-m\) vô nghiệm trên \(\left(-\infty;-2\right)\)
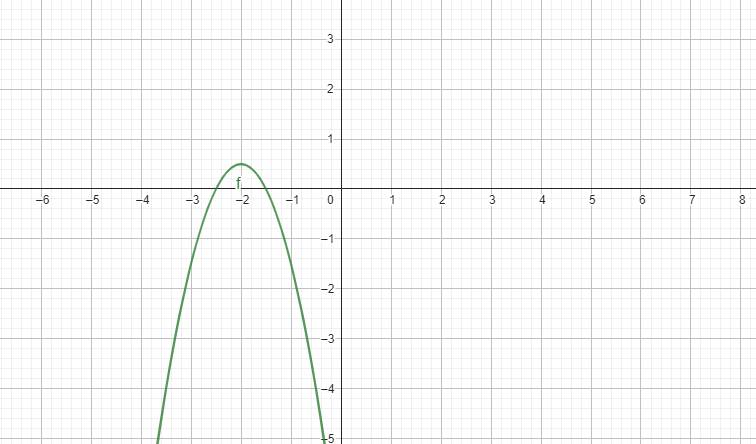
Xét hàm \(f\left(x\right)=x^2-2x-3\) khi \(x< -2\)
\(a=1>0;-\dfrac{b}{2a}=1>-2\)
\(\Rightarrow f\left(x\right)\) nghịch biến khi \(x< -2\)
\(\Rightarrow f\left(x\right)>f\left(-2\right)=5\)
\(\Rightarrow\) Pt vô nghiệm khi \(-m\le5\Rightarrow m\ge-5\)