Cho tam giác ABC. Kéo dài BC thêm một doạn CD = BC x 2. Nối A với D. So sánh diện tích 2 tam giác ADB và ABC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
giúp mình mình cho một like
A
5 tháng 1 2022
Giải thích các bước giải:
Chiều cao của tam giác BCA cũng chính là chiều cao tam giác ABD
Diện tích ABC = 1/2x chiều cao x BC
Diện tích phần tăng thêm = diện tích ACD = 1/2 x chiều cao x CD = 1/4 x chiều cao xBC = 20
=> Diện tích tam giác ABC là
20 x 2= 40 dm^2
Đ/S :.......
22 tháng 5 2023
a: S ABE=S EBD=1/2*S ABD
DC=1/2DB
nên S ADC=1/2*S ABD
=>S ABE=S EBD=S ADC
b: S ABC=3/2*24=36cm2
S
7 tháng 2 2016
25% = 1/4
đáy CD = 1/4 BC
diện tích ACD = 240 : 4 = 60
diện tích ABD = 240 + 60 = 300
21 tháng 5 2023
a) Đáy lớn CD là : 8:2/3= 12 (cm)
Diện tích hình thang ABCD là: ( 8+12):2.15= 150(cm2)
b) Vì đáy bé AB < đáy lớn CD ( vì 8cm < 12cm)
=> S ABC < S ACD
c) từ D kẻ đường thẳng song song với AC cắt BC tại E tạo thành một hình tam giác
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
25 tháng 6 2023
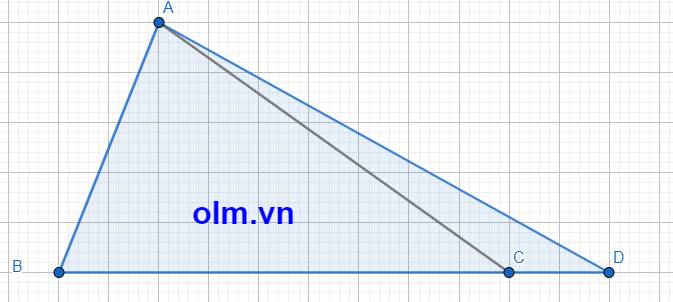
BD = BC + CD = BC + \(\dfrac{2}{9}\)BC = \(\dfrac{11}{9}\)BC
SABD = \(\dfrac{11}{9}\)SABC ( vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và BD = \(\dfrac{11}{9}\)BC)
Diện tích tam giác ABD là:
351 \(\times\) \(\dfrac{11}{9}\) = 429 (cm2)
Đáp số: 429 (cm2)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
25 tháng 6 2023
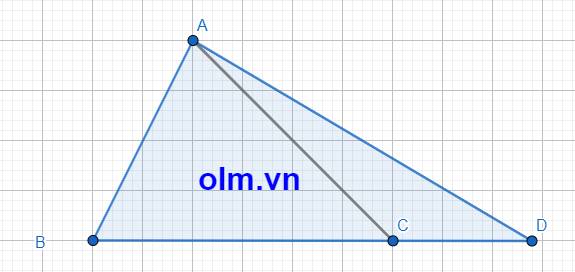
CD = BC + CD = BC + \(\dfrac{6}{13}\)BC = \(\dfrac{19}{13}\)BC
SABD = \(\dfrac{19}{13}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và AD = \(\dfrac{19}{13}\)BC)
Diện tích tam giác ABD là: 481 \(\times\)\(\dfrac{19}{13}\) = 703(cm2)
Đáp số: 703 cm2
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
25 tháng 5 2022
a/
Ta có
\(NC=2AN\Rightarrow\dfrac{AN}{AC}=\dfrac{1}{3}\)
Hai tg ABN và tg ABC có chung đường cao từ B->AC nên
\(\dfrac{S_{ABN}}{S_{ABC}}=\dfrac{AN}{AC}=\dfrac{1}{3}\Rightarrow S_{ABN}=\dfrac{1}{3}xS_{ABC}\)
Hai tg DBN và tg DCN có chung đường cao từ D->BC và BM=CM nên
đường cao từ B->DM = đường cao từ C->DM
Hai tg DNA và tg DNC có chung đường cao từ D->AC nên
\(\dfrac{S_{DNA}}{S_{DNC}}=\dfrac{AN}{CN}=\dfrac{1}{2}\)
Hai tg này lại có chung DN nên
\(\dfrac{S_{DNA}}{S_{DNC}}=\) đường cao từ A->DM / đường cao từ C->DM \(=\dfrac{1}{2}\)
=> đường cao từ A->DM / đường cao từ B->DM \(=\dfrac{1}{2}\)
Hai tg DNA và tg DBN có chung DN nên
\(\dfrac{S_{DNA}}{S_{DBN}}=\) đường cao từ A->DM / đường cao từ B->DM \(=\dfrac{1}{2}\)
\(\Rightarrow S_{DBN}=2xS_{DNA}\)
\(\Rightarrow S_{DNA}=S_{DBN}-S_{ABN}=2xS_{DNA}-S_{DBN}\Rightarrow S_{DNA}=S_{ABN}=\dfrac{1}{3}xS_{ABC}=\dfrac{10}{3}cm^2\)
b/
Hai tg DNB và tg DNC có chung DN và đường cao từ B->DM = đường cao từ C->DM nên
\(S_{DNB}=S_{DNC}\)
c/ Hai tg DNA và tg ABN có chung đường cao từ N->DB nên
\(\dfrac{S_{DNA}}{S_{ABN}}=\dfrac{AD}{AB}=1\)