Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2:
Gọi AC là chiều cao của cây, AB là bóng của cây trên mặt đất
=>AC\(\perp\)AB tại A
Theo đề, ta có: AB=4,5m và \(\widehat{B}=50^0\)
Xét ΔABC vuông tại A có
\(tanB=\dfrac{AC}{AB}\)
=>\(\dfrac{AC}{4.5}=tan50\)
=>\(AC=4,5\cdot tan50\simeq5,36\left(m\right)\)

Phần cây bị gãy tạo với mặt đất và phần còn lại một tam giác vuông.
Gọi gốc cây cột điện là A, điểm bị gãy là B và điểm chạm đất là C, ta có:
Tam giác ABC vuông tại A, AB = 3m; AC = 4m
Áp dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2=3^2+4^2=25\Rightarrow BC=5\left(m\right)\)
Chiều cao cột điện ban đầu là: \(AB+BC=3+5=8\left(m\right)\)

Giả sử gốc là điểm A, điểm gãy là B và điểm ngọn chạm đất là C, ta có tam giác ABC vuông tại A
Trong đó \(AC=3m\) ; \(AB+BC=9\left(m\right)\)
Áp dụng định lý Pitago:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AB^2+3^2=\left(9-AB\right)^2\)
\(\Leftrightarrow9=81-18AB\)
\(\Rightarrow AB=4\left(m\right)\)
Vậy điểm gãy cách gốc 4m

gọi k/c từ điểm gãy đến ngọn cây là x . Vì cây cau vuông góc với mặt đất nên cây cau gãy tạo với mặt đất hình tam giác vuông =>khoảng cách từ gốc đến điểm gãy và k/c từ ngọn cây đến góc là cạnh góc vuông và x là cạnh huyền Định Lí PTG ta có : 3^2+4^2=x^2 =>x=5 => chiều cao cây = 5+4=9m

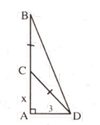
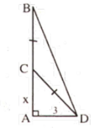
Giả sử AB là độ cao của cây tre, C là điểm gãy.
Đặt AC = x (0 < x < 9) => CB = CD = 9 – x.
Vì ∆ ACD vuông tại A
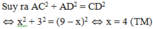
Vậy điểm gãy cách gốc cây 4m
Đáp án cần chọn là: C


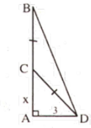
Giả sử AB là độ cao của cây tre, C là điểm gãy.
Đặt AC = x CB = CD = 8 – x.
Vì ∆ ACD vuông tại A
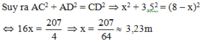
Vậy điểm gãy cách gốc cây 3,23m
Đáp án cần chọn là: B


Gọi chiều dài phần trên gãy ngang là c
Áp dụng định lí Py-ta-go ta được: 52 + 122 = c2
=> c2 = 169 => c = 13m
Cây cột điện dài : 13 + 5 = 18m
Chiều cao của phần bị gãy là:
√(5^2 + 12^2) = 13 (m)
Chiều cao của cây cột điện là:
13 + 5 = 18 (m)
Vậy cây cột điện cao 18m