Câu 6: Cho ∆ABC nhọn (AB < AC), M là trung điểm BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh: ∆MAB = ∆MDC
b) Chứng minh: AB // CD
Trên các đoạn thẳng AB, CD lần lượt lấy các điểm G và H sao cho AG = DH. Chứng minh: ba điểm G, M, H thẳng hàng


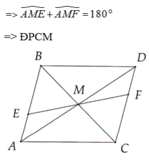
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB//CD