Tam giác ABC vuông tại A, góc C =60, AB=\(\sqrt{192}\)Cho em hỏi làm thế nào để tính diện tích tam giác ABC vậy ạ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


AB^2+AC^2=BC^2
AC^2+ CĂN 192=4AC^2 (VÌ AC =1/2 BC)
SUY RA 3AC^2=CĂN 192
SUY RA AC^2=\(\frac{\sqrt{192}}{3}\)
SUY RA AC=

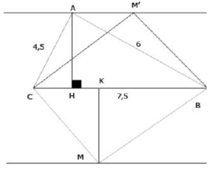
a) Ta có: A B 2 + A C 2 = 6 2 + 4 , 5 2 = 7 , 5 2 = B C 2
nên tam giác ABC vuông tại A. (đpcm)
![]()
= > ∠ B = 37 ° = > ∠ C = 90 ° - ∠ B = 90 ° - 37 ° = 53 °
Mặt khác trong tam giác ABC vuông tại A, ta có:
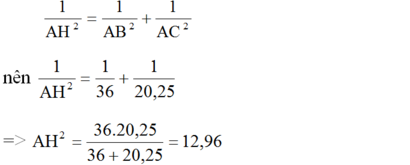
=> AH = 3,6 cm
b) Gọi khoảng cách từ M đến BC là MK. Ta có:
![]()
Ta thấy SMBC = SABC khi MK = AH = 3,6 cm
Do đó để SMBC = SABC thì M phải nằm trên đường thẳng song song và cách BC một khoảng là 3,6 cm (có hai đường thẳng như trên hình).

a, Xét \(\Delta\)ABC có: AB2 + AC2 = 62 + 4,52 = 56,25 (cm2)
BC2 = 7,52 = 56,25 (cm2)
AB2 + AC2 = BC2 vậy tam giác ABC vuông tại A (đpcm)
SinC = 6 : 7,5 =0,8 ⇒ \(\widehat{C}\) = 53,130 ⇒ \(\widehat{B}\) = 900 - 53,130 = 36,870
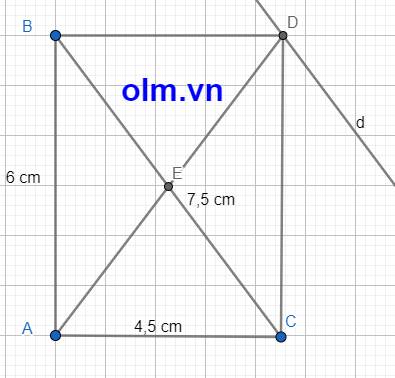
b, Dựng hình chữ nhật ABCD, chiều cao AH, DK, và đường thẳng d đi qua D song song với BC như hình vẽ ta có
SABC = SBDC ⇒ AH = DK
Lây 1 điểm bất M kỳ di động trên đường thẳng d ta có:
SBDC = SMBC (vì hai tam giác có chiều cao bằng nhau và chung cạnh đáy BC)
⇒ SABC = SMBC
Kết luận khi M di động trên đường thẳng d thì diện tích tam giác MBC luôn bằng diện tích tam giác ABC
Xét ΔABC vuông tại A có
\(AC=AB\cdot\cot\widehat{C}\)
\(\Leftrightarrow AC=\sqrt{192}\cdot\cot60^0=8\left(cm\right)\)
Ta có: ΔABC vuông tại A(gt)
nên \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{8\sqrt{3}\cdot8}{2}=32\sqrt{3}\left(cm^2\right)\)