Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC vuông tại A có
\(AC=AB\cdot\cot\widehat{C}\)
\(\Leftrightarrow AC=\sqrt{192}\cdot\cot60^0=8\left(cm\right)\)
Ta có: ΔABC vuông tại A(gt)
nên \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{8\sqrt{3}\cdot8}{2}=32\sqrt{3}\left(cm^2\right)\)

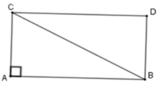
Vì ABDC là hình chữ nhật nên SABDC = AC. AB
mà SABC = A C . A B 2 nên SABCD = 2SABC
= 2.140 = 280 cm2.
Đáp án cần chọn là: B

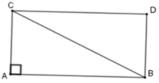
Vì ABDC là hình chữ nhật nên SABDC = AC. AB
mà SABC = A C . A B 2 nên SABCD = 2SABC
= 2.55 = 110 cm2.
Đáp án cần chọn là: A

Vì tam giác ABC vuông tại A mà góc C=60 độ
=>AC=1/2 BC
Từ đây áp dụng py ta gô mà giải thui bạn ak
Nếu thấy bài làm của mình đúng thì tick nha bạn.Cảm ơn bạn nhiều.

AB^2+AC^2=BC^2
AC^2+ CĂN 192=4AC^2 (VÌ AC =1/2 BC)
SUY RA 3AC^2=CĂN 192
SUY RA AC^2=\(\frac{\sqrt{192}}{3}\)
SUY RA AC=

\(S=\dfrac{12\cdot9}{2}=6\cdot9=54\left(cm^2\right)\)