Làm tự luận giúp m với ạ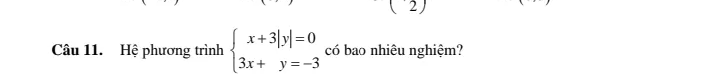
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LL
Làm dưới dạng tự luận ( giúp mình với ạ :< )
0
31 tháng 10 2021
Câu 1:
a: \(\sqrt{9\cdot25}=3\cdot5=15\)
b: \(=3\sqrt{2}\cdot\sqrt{2}+4\sqrt{2}\cdot\sqrt{2}-5\sqrt{2}\cdot\sqrt{2}\)
=6+8-10
=4
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 8 2021
1.
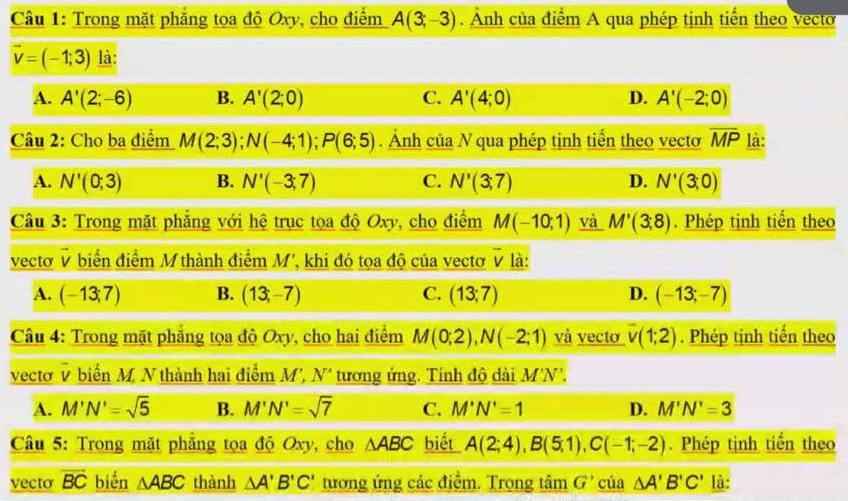
\(\left\{{}\begin{matrix}x_{A'}=x_A+\left(-1\right)=2\\y_{A'}=y_A+3=0\end{matrix}\right.\) \(\Rightarrow A'\left(2;0\right)\)
2.
\(\overrightarrow{MP}=\left(4;2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_{N'}=x_N+4=-4+4=0\\y_{N'}=y_N+2=1+2=3\end{matrix}\right.\)
\(\Rightarrow N'\left(0;3\right)\)
3.
\(\overrightarrow{MM'}=\left(13;7\right)\Rightarrow\overrightarrow{v}=\overrightarrow{MM'}=\left(13;7\right)\)
4.
\(\overrightarrow{MN}=\left(-2;-1\right)\Rightarrow MN=\sqrt{\left(-2\right)^2+\left(-1\right)^2}=\sqrt{5}\)
\(\Rightarrow M'N'=MN=\sqrt{5}\)
5.
Gọi G là trọng tâm ABC \(\Rightarrow G\left(2;1\right)\)
\(\overrightarrow{BC}=\left(-6;-3\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_{G'}=2-6=-4\\y_{G'}=1-3=-2\end{matrix}\right.\) \(\Rightarrow G'\left(-4;-2\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 7 2021
18.
Do D thuộc trục hoành nên tọa độ có dạng: \(D\left(a;0;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AD}=\left(a-3;4;0\right)\\\overrightarrow{BC}=\left(4;0;-3\right)\end{matrix}\right.\)
\(AD=BC\Leftrightarrow\left(a-3\right)^2+4^2=4^2+\left(-3\right)^2\)
\(\Rightarrow\left(a-3\right)^2=9\Rightarrow\left[{}\begin{matrix}a=0\\a=6\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}D\left(0;0;0\right)\\D\left(6;0;0\right)\end{matrix}\right.\)
19.
\(cos\left(\overrightarrow{a};\overrightarrow{b}\right)=\dfrac{2.\left(-1\right)+1.0+0.\left(-2\right)}{\sqrt{2^2+1^2+0^2}.\sqrt{\left(-1\right)^2+0^2+\left(-2\right)^2}}=-\dfrac{2}{5}\)
20.
\(\overrightarrow{OA}=\left(2;2;1\right)\Rightarrow OA=\sqrt{2^2+2^2+1^2}=3\)
TG
0
NV
4
HP
27 tháng 3 2021
1.
\(cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{1}{2}\Rightarrow\widehat{A}=60^o\)
\(S=\dfrac{1}{2}bc.sinA=\dfrac{1}{2}.8.5.sin60^o=10\sqrt{3}\)
\(S=\dfrac{1}{2}a.h_a=\dfrac{1}{2}.7.h_a=10\sqrt{3}\Rightarrow h_a=\dfrac{20\sqrt{3}}{7}\)
\(2R=\dfrac{a}{sinA}=\dfrac{7}{\dfrac{\sqrt{3}}{2}}=\dfrac{14\sqrt{3}}{3}\Rightarrow R=\dfrac{7\sqrt{3}}{3}\)
\(S=pr=\dfrac{a+b+c}{2}.r=10r=10\sqrt{3}\Rightarrow r=\sqrt{3}\)
\(m_a^2=\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}=\dfrac{129}{4}\Rightarrow m_a=\dfrac{\sqrt{129}}{2}\)
HP
27 tháng 3 2021
6.
a, Công thức trung tuyến:
\(AM^2=c^2=\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}=\dfrac{2b^2+2c^2-a^2}{4}\Rightarrow a^2=2\left(b^2-c^2\right)\)
b, \(a^2=2\left(b^2-c^2\right)\Rightarrow\dfrac{2\left(b^2-c^2\right)}{a^2}=1\)
\(\Leftrightarrow2\left(\dfrac{b^2}{a^2}-\dfrac{c^2}{a^2}\right)=1\)
\(\Leftrightarrow2\left(\dfrac{b^2}{a^2}.sin^2A-\dfrac{c^2}{a^2}.sin^2A\right)=sin^2A\)
\(\Leftrightarrow2\left(sin^2B-sin^2C\right)=sin^2A\)
Hay \(sin^2A=2\left(sin^2B-sin^2C\right)\)
TG
0
giúp em trắc nghiệm thui ạ tự luận em tự làm cảm ơn ạ
KV
18 tháng 10 2023
Dạng 1
Đại số
Câu 1. B
Câu 2. B
Câu 3. D
Câu 4. B
Câu 5. B
Câu 6. C
Lời giải:
HPT \(\Leftrightarrow \left\{\begin{matrix} x=-3|y|\\ 3x+y=-3\end{matrix}\right.\)
\(\Rightarrow -9|y|+y=-3\)
Nếu $y\geq 0$ thì pt trở thành:
$-9y+y=-3$
$\Leftrightarrow y=\frac{3}{8}$
$x=-3|y|=-3.\frac{3}{8}=\frac{-9}{8}$
Nếu $y< 0$ thì pt trở thành:
$9y+y=-3\Leftrightarrow y=\frac{-3}{10}$
$x=-3|y|=-3.\frac{3}{10}=\frac{-9}{10}$
Vậy hpt có 2 nghiệm $(x,y)=(\frac{3}{8}, \frac{-9}{8}); (\frac{-3}{10}, \frac{-9}{10})$