Bài 9. Hình thang ABCD có các đáy AB và CD theo thứ tự dài 12cm và 30cm, các cạnh bên AD và BC theo thứ tự dài 9cm và 15cm. Các đường thẳng AD và BC cắt nhau ở O. Tính các độ dài OA, OB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 6 2017
Ta có: BC // HK, BH // CK (cùng \(\perp\) AD)
=> \(\left\{{}\begin{matrix}BC=HK=9cm\\BH=CK=a\end{matrix}\right.\) (tính chất đoạn chắn)
Có: b + HK + c = AD
=> b + 9 + c = 30
=> b + c = 21
Áp dụng định lí Py-ta-go ta có: \(\left\{{}\begin{matrix}a^2+b^2=AB^2=20^2\\a^2+c^2=CD^2=13^2\end{matrix}\right.\)
Từ vế với vế ta được: b2 - c2 = 202 - 132
=> (b - c)(b + c) = 231
=> (b - c).21 = 231
=> b - c = 11
Mà b + c = 21 nên \(\left\{{}\begin{matrix}c=\dfrac{21-11}{2}=5=KD\\b=21-5=16=AH\end{matrix}\right.\)
UI
11 tháng 9 2019
Ban tu ve hinh nha, cau b va cau c mik gop lai lam chung 1 phan nha,
a) Do E la trung diem AD va F la trung diem BC nen EF la duong trung binh hing thang ABCD => AB//EF//DC
Do AB//EF =>\(\widehat{BAI}=\widehat{AIE}\left(Soletrong\right)\)ma \(\widehat{EAI}=\widehat{BAI}\left(AI.la.tia.phan.giac\right)\)
Suy ra \(\widehat{EAI}=\widehat{EIA}=>\Delta AIE.can.tai.E\)
chung minh tam giac BKE can tuong tu nha
b)+c) : do \(\Delta EAI.can\left(cma\right)\Rightarrow EA=EI\) ma EA=ED(gt)
Suy ra EA=ED=EI =>\(\Delta ADI\perp tai.I\) ( Ap dung dinh ly tam giac co duong trung tuyen ung voi canh doi dien va = 1/2 canh do thi la tam giac vuong )
chung minh tam giac BKC vuong tuong tu
Tu do ta cung suy ra luon duoc IE=1/2AD (vi cung =AE) ; KF=1/2BC thi tuong tu
d) Do ABCD la hinh thnag co EF la duong trung binh nen \(EF=\frac{AB+DC}{2}\Leftrightarrow EI+IK+KF=\frac{5+18}{2}=11,5.\left(1\right)\)
Ma ta da co EI=EA=ED(cmt) => EI=EA=6/2=3 cm , KF=BF=FC (cmt) => KF=BF=7/2=3,5 cm
Thay vao (1) ta co \(3+3,5+IK=11,5\Rightarrow IK=5\left(cm\right)\)
Vay IK=5 cm
Chuc ban hoc tot
CH
Cô Hoàng Huyền
Admin
VIP
26 tháng 2 2018
Qua N kẻ đường thẳng NP // AB (P thuộc BC)
Khi đó ta thấy ngay \(\Delta EBN=\Delta PNB\left(g-c-g\right)\Rightarrow EB=PN;EN=PB\) (1)
Do NP // AB nên \(\widehat{NPC}=\widehat{EPB}\); do DM // BC nên \(\widehat{ADM}=\widehat{EPB}\)
Suy ra \(\widehat{ADM}=\widehat{NPC}\)
Ta cũng có \(\widehat{DAM}=\widehat{PNC}\) (Hai góc đồng vị)
\(\Rightarrow\Delta DAM=\Delta PNC\left(g-c-g\right)\)
\(\Rightarrow AM=PC\) (2)
Từ (1) và (2) suy ra DM + EN = PC + BP = BC.
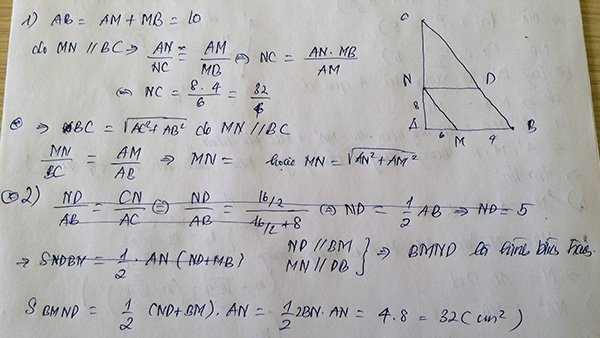
Ta có AB//CD (2 đáy của hình thang ABCD)
\(\Rightarrow\frac{OA}{OD}=\frac{OB}{OC}=\frac{AB}{CD}\Rightarrow\frac{OA}{OA+AD}=\frac{OB}{OB+BC}=\frac{AB}{CD}\)
Từ \(\frac{OA}{OA+AD}=\frac{AB}{CD}\Rightarrow\frac{OA}{OA+9}=\frac{12}{30}\Rightarrow AO=6cm\)
Từ \(\frac{OB}{OB+BC}=\frac{AB}{CD}\Rightarrow\frac{OB}{OB+15}=\frac{12}{30}\Rightarrow OB=10cm\)