Cho đoạn thẳng AB. Đường trung trực d của BC cắt BC tại H. Gọi M là 1 điểm của đường thẳng d ( M khác H ). Chứng minh Δ BHM = Δ CHM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
14 tháng 8 2023
a/
Xét tg vuông ABE và tg vuông HBE có
BE chung
\(\widehat{ABE}=\widehat{HBE}\) (gt)
=> tg ABE = tg HBE (Hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau)
b/
tg ABE = tg HBE (cmt) => AB = HB => tg BAH cân tại B
\(\widehat{ABE}=\widehat{HBE}\)
=> BE là trung trực của AH (Trong tg cân đường phân giác của góc ở đỉnh tg cân đồng thời là đường trung trực)
c/
Xét tg vuông KBH và tg vuông ABC có
\(\widehat{B}\) chung
AB = HB (cmt)
=> tg KBH = tg ABC (Hai tg vuông có cạnh góc vuông và góc nhọn tương ứng bằng nhau) => BK=BC
Xét tg BKE và tg BCE có
BE chung
\(\widehat{ABE}=\widehat{HBE}\) (gt)
BK=BC (cmt)
=> tg BKE = tg BCE (c.g.c) => EK = EC
d/
Xét tg vuông AKE có
AE<EK (trong tg vuông cạnh huyền là cạnh có độ dài lớn nhất
Mà EK=EC (cmt)
=> AE<EC
AT
23 tháng 11 2016
Ta có hình vẽ sau:
a) \(\widehat{AHB}\) = \(\widehat{DHB}\) = \(\frac{180^o}{2}\) = 90o (2 góc kề bù)
Xét ΔABH và ΔDBH có:
BH là cạnh chung
\(\widehat{AHB}\) = \(\widehat{DHB}\) = 90o (cm trên)
AH = DH (gt)
=> ΔABH = ΔDBH (c.g.c) (đpcm)
b) Vì ΔABH = ΔDBH (ý a)
=> \(\widehat{B_1}\) = \(\widehat{B_2}\) ( 2 góc tương ứng)
= BC là tia phân giác của \(\widehat{ABD}\) (đpcm)
c) Vì ΔABH = ΔDBH => AB = DB (2 cạnh tương ứng)
Xét ΔABC và ΔDBC có:
BC là cạnh chung
\(\widehat{B_1}\) = \(\widehat{B_2}\) (ý b)
AB = DB (cm tên)
=> ΔABC = ΔDBC(c.g.c)
=> \(\widehat{BAC}\) = \(\widehat{BDC}\) (2 góc tương ứng) (đpcm)
d) Vì ΔABH = ΔDBH (ý a)
=> AB = DB => \(\frac{1}{2}\)AB = \(\frac{1}{2}\)DB
=> NB = ND = \(\frac{1}{2}\)DB
=> N là trung điểm của BD(đpcm)
22 tháng 2 2022
a: Xét ΔABH vuông tại H và ΔDBH vuông tại H có
HB chung
HA=HD
Do đó: ΔABH=ΔDBH
b: Ta có: ΔABH=ΔDBH
nên \(\widehat{ABH}=\widehat{DBH}\)
hay BC là tia phân giác của góc ABD
24 tháng 11 2016
Ta có hình vẽ:
a/ Xét tam giác ABH và tam giác DBH có:
BH: cạnh chung
\(\widehat{AHB}\)=\(\widehat{DHB}\)=900 (GT)
AH = HD (GT)
Vậy tam giác ABH = tam giác DBH (c.g.c)
b/ Ta có: tam giác ABH = tam giác DBH (câu a)
=> \(\widehat{ABH}\)=\(\widehat{DBH}\)( 2 góc tương ứng)
=> \(\widehat{ABC}\)=\(\widehat{DBC}\)
=> BC là phân giác của góc ABD (đpcm)
c/ Xét tam giác ABC và tam giác DBC có:
BC: cạnh chung
\(\widehat{ABC}\)=\(\widehat{DBC}\) (đã chứng minh)
AB = DB (vì tam giác ABH = tam giác DBH)
=> tam giác ABC = tam giác DBC (c.g.c)
=>\(\widehat{BAC}\)=\(\widehat{BDC}\)(2 góc tương ứng)
d/ Ta có: AB = DB (vì tam giác ABH = tam giác DBH)
Mà BM = AM
=> BN = DN
\(\Rightarrow\) Vậy N là trung điểm BD (đpcm)
22 tháng 2 2022
a: Xét ΔABH vuông tại H và ΔDBH vuông tại H có
HB chung
HA=HD
Do đó: ΔABH=ΔDBH
b: Ta có: ΔABH=ΔDBH
nên \(\widehat{ABH}=\widehat{DBH}\)
hay BC là tia phân giác của góc ABD
c: Xét ΔACD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔACD cân tại C
Xét ΔBAC và ΔBDC có
BA=BD
AC=DC
BC chung
DO đó: ΔBAC=ΔBDC
Suy ra: \(\widehat{BAC}=\widehat{BDC}\)
16 tháng 4 2023
\(\text{#TNam}\)
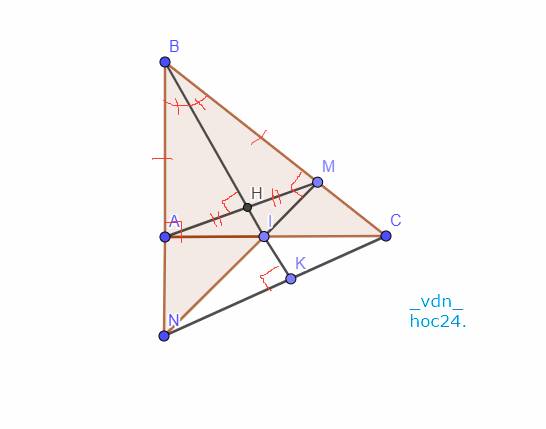
`a,`
Xét Tam giác `ABI` và Tam giác `MBI` có:
`\text {BI chung}`
\(\widehat{ABI}=\widehat{MBI} (\text {tia phân giác}\) \(\widehat{ABM} )\)
\(\widehat{BAI}=\widehat{BMI}=90^0\)
`=> \text {Tam giác ABI = Tam giác MBI (ch-gn)}`
`=> BA = BM (\text {2 cạnh tương ứng})`
Gọi `H` là giao điểm của `BI` với `AM`
Xét Tam giác `HAB` và Tam giác `HMB` có:
\(\text{BA = BM (CMT)}\)
\(\widehat{ABH}=\widehat{MBH} (\text {tia phân giác} \widehat{ABM})\)
`\text {BH chung}`
`=> \text {Tam giác HAB = Tam giác HMB (c-g-c)}`
`-> \text {HA = HM (2 cạnh tương ứng)}`
`->`\(\widehat{BHA}=\widehat{BHM} (\text {2 góc tương ứng})\)
Mà `2` góc này nằm ở vị trí kề bù
`->`\(\widehat{BHA}+\widehat{BHM}=180^0\)
`->`\(\widehat{BHA}=\widehat{BHM}=\)`180/2=90^0`
`-> \text {BH} \bot \text {AM}`
Ta có: \(\left\{{}\begin{matrix}BH\perp AM\\HA=HM\end{matrix}\right.\)
`->` \(\text{BI là đường trung trực của AM.}\)
`b,`
Xét Tam giác `BAC` và Tam giác `BMN` có:
\(\widehat{B} \) `\text {chung}`
`BA = BM (a)`
\(\widehat{BAC}=\widehat{BMN}=90^0\)
`=> \text {Tam giác BAC = Tam giác BMN (g-c-g)}`
`-> \text {BN = BC (2 cạnh tương ứng)}`
Xét Tam giác `BIN` và Tam giác `BIC` có:
`BN = BC (CMT)`
\(\widehat{NBI}=\widehat{CBI} (\text {tia phân giác} \widehat{NBC})\)
`\text {BI chung}`
`=> \text {Tam giác BIN = Tam giác BIC (c-g-c)}`
`-> \text {IN = IC (2 cạnh tương ứng)}`
`c,`
Gọi `K` là giao điểm của `BI` và `NC`
Xét Tam giác `NBK` và Tam giác `CBK` có:
`BN = BC (CMT)`
\(\widehat{NBK}=\widehat{CBK} (\text {tia phân giác} \widehat{NBC})\)
`\text {BK chung}`
`=> \text {Tam giác NBK = Tam giác CBK (c-g-c)}`
`->`\(\widehat{BKN}=\widehat{BKC} (\text {2 góc tương ứng})\)
Mà `2` góc này nằm ở vị trí kề bù
`->`\(\widehat{BKN}+\widehat{BKC}=180^0\)
`->`\(\widehat{BKN}=\widehat{BKC}=\)`180/2=90^0`
`-> \text {BK} \bot \text {NC}`
`-> \text {BI} \bot \text {NC (đpcm)}`
