Chứng minh rằng: (a + b)( a 2 – ab + b 2 ) + (a – b)( a 2 + ab + b 2 ) = 2 a 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 8 2016
a)a2+b2+c2+3=2(a+b+c)
=>a2+b2+c2+1+1+1-2a-2b-2c=0
=>(a2-2a+1)+(b2-2b+1)+(c2-2c+1)=0
=>(a-1)2+(b-1)2+(c-1)2=0
=>a-1=b-1=c-1=0 <=>a=b=c=1
-->Đpcm
b)(a+b+c)2=3(ab+ac+bc)
=>a2+b2+c2+2ab+2ac+2bc -3ab-3ac-3bc=0
=>a2+b2+c2-ab-ac-bc=0
=>2a2+2b2+2c2-2ab-2ac-2bc=0
=>(a2- 2ab+b2)+(b2-2bc+c2) + (c2-2ca+a2) = 0
=>(a-b)2+(b-c)2+(c-a)2=0
Hay (a-b)2=0 hoặc (b-c)2=0 hoặc (a-c)2=0
=>a-b hoặc b=c hoặc a=c
=>a=b=c
-->Đpcm
c)a2+b2+c2=ab+bc+ca
=>2(a2+b2+c2)=2(ab+bc+ca)
=>2a2+2b2+c2=2ab+2bc+2ca
=>2a2+2b2+c2-2ab-2bc-2ca=0
=>a2+a2+b2+b2+c2+c2-2ab-2bc-2ca=0
=>(a2-2ab+b2)+(b2-2bc+c2)+(a2-2ca+c2)=0
=>(a-b)2+(b-c)2+(a-c)2=0
Hay (a-b)2=0 hoặc (b-c)2=0 hoặc (a-c)2=0
=>a-b hoặc b=c hoặc a=c
=>a=b=c
-->Đpcm
MN
3
TP
29 tháng 6 2017
b, ta có a3+ b3 = (a+b)(a2-ab +b2)
= (a+b)(a2 -ab +b2 -ab +ab)
= (a+b) ( a2-2ab +b +ab)
=(a+b) [ (a2-b2) +ab ]
vậy ...........................
M
1
31 tháng 8 2015
VT = ( a + b )(a^2 - ab + b^2) + ( a- b)(a^2 + ab + b^2)
= a^3 + b^3 + a^3 - b^3
= 2a^3
=VP
=> ĐPCM
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
24 tháng 9 2015
1/
\(\left(1\right)=\left(a^3+b^3\right)+\left(a^3-b^3\right)=2a^3\)
2/
\(\left(2\right)=a^3+b^3=\left(a+b\right).\left(a^2-ab+b^2\right)\)
\(\left(2\right)=\left(a+b\right).\left[\left(a^2-2ab+b^2\right)+ab\right]=\left(a+b\right)\left[\left(a-b\right)^2+ab\right]\)
3/
\(\left(3\right)=\left(ac\right)^2+\left(ad\right)^2+\left(bc\right)^2+\left(bd\right)^2\)
\(\left(3\right)=\left[\left(ac\right)^2+2acbd+\left(bd\right)^2\right]+\left[\left(ad\right)^2-2adbc+\left(bc\right)^2\right]\)(do t/c giao hoán trong phép nhân => 2acbd=2adbc)
\(\left(3\right)=\left(ac+bd\right)^2+\left(ad-bc\right)^2\)
20 tháng 3 2018
a)\(a^2+ab+b^2=a^2+\dfrac{2ab}{2}+\left(\dfrac{b}{2}\right)^2+\dfrac{3b^2}{4}\)
\(=\left(a+\dfrac{b}{2}\right)^2+\dfrac{3b^2}{4}\ge0\forall a,b\)
b)\(a^4+b^4\ge a^3b+ab^3\)
\(\Leftrightarrow a^3\left(a-b\right)-b^3\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a^3-b^3\right)\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\left(a^2+ab+b^2\right)\ge0\forall a,b\)
TT
1
DT
13 tháng 7 2016
ap dung hang dang thuc
(a^3+b^3)+(a^3-b^3)=a^3+b^3+a^3-b^3=2a^3 (dpcm)
LD
23 tháng 7 2019
a. \(2\left(a^2+b^2\right)=\left(a-b\right)^2\)
\(\Leftrightarrow2a^2+2b^2=a^2+b^2-2ab\)
\(\Leftrightarrow a^2+b^2=-2ab\)
\(\Leftrightarrow a^2+2ab+b^2=0\)
\(\Leftrightarrow\left(a+b\right)^2=0\)
\(\Leftrightarrow a+b=0\Leftrightarrow a=-b\) (đpcm)
b. \(a^2+b^2+c^2+3=2\left(a+b+c\right)\)
\(\Leftrightarrow a^2+b^2+c^2+3-2a-2b-2c=0\)
\(\Leftrightarrow\left(a^2-2a+1\right)+\left(b^2-2b+1\right)+\left(c^2-2c+1\right)=0\)
\(\Leftrightarrow\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2=0\)
Vì \(\left(a-1\right)^2;\left(b-1\right)^2;\left(c-1\right)^2\ge0\)
\(\Rightarrow\left(a-1\right)^2=\left(b-1\right)^2=\left(c-1\right)^2=0\)
\(\Leftrightarrow a-1=b-1=c-1=0\Leftrightarrow a=b=c=1\)
c. \(\left(a+b+c\right)^2=3\left(ab+bc+ca\right)\)
\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=3\left(ab+bc+ca\right)\)
\(\Leftrightarrow a^2+b^2+c^2=ab+bc+ca\)
\(\Leftrightarrow2\left(a^2+b^2+c^2\right)=2\left(ab+bc+ca\right)\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
Tương tự câu b ta có a = b = c
8 tháng 10 2016
Ta có a3 + b3 - ab(a + b) \(\ge0\)
\(\Leftrightarrow\)(a + b)(a2 - ab + b2 - ab)\(\ge0\)
\(\Leftrightarrow\)(a + b)(a - b)2 \(\ge0\)(đúng)
Vậy cái ban đầu là đúng
PT
13 tháng 9 2017
a) \(\left(a+b\right)\left(a^2-ab+b^2\right)+\left(a-b\right)\left(a^2+ab+b^2\right)\)
=\(a^3+b^3+\left(a^3-b^3\right)\)
=\(a^3+b^3+a^3-b^3\)
=\(2a^3\)
b) \(a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)\)
=\(\left(a+b\right)\left(a^2-2ab+b^2-ab\right)\)
=\(\left(a+b\right)\left[\left(a^2-2ab+b^2\right)-ab\right]\)
=\(\left(a+b\right)\left[\left(a-b\right)^2-ab\right]\)
13 tháng 9 2017
a. \(\left(a+b\right)\left(a^2-ab+b^2\right)+\left(a-b\right)\left(a^2+ab+b^2\right)=a^3+b^3+a^3-b^3=2a^3\)
b. \(a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)=\left(a+b\right)\left(a^2-2ab+b^2+ab\right)=\left(a+b\right)\left[\left(a-b\right)^2+ab\right]\)
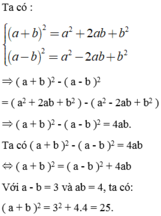
Biến đổi vế trái ta có:
VT = (a + b)( a 2 – ab + b 2 ) + (a – b)( a 2 + ab + b 2 )
= a 3 + b 3 + a 3 – b 3 = 2 a 3 = VP
Vế trái bằng vế phải nên đẳng thức được chứng minh.