Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
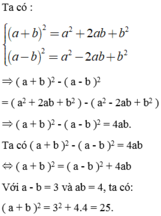
b, Ta có \(m=a+b+c\)
\(\Rightarrow am+bc=a\left(a+b+c\right)+bc=a\left(a+b\right)+ac+bc=\left(a+c\right)\left(a+b\right)\)
CMTT \(bm+ac=\left(b+c\right)\left(b+a\right)\);\(cm+ab=\left(c+a\right)\left(c+b\right)\)
Suy ra \(\left(am+bc\right)\left(bm+ac\right)\left(cm+ab\right)=\left(a+b\right)^2\left(a+c\right)^2\left(b+c\right)^2\)
+ Chứng minh (a + b)2 = (a – b)2 + 4ab
Ta có:
VP = (a – b)2 + 4ab = a2 – 2ab + b2 + 4ab
= a2 + (4ab – 2ab) + b2
= a2 + 2ab + b2
= (a + b)2 = VT (đpcm)
+ Chứng minh (a – b)2 = (a + b)2 – 4ab
Ta có:
VP = (a + b)2 – 4ab = a2 + 2ab + b2 – 4ab
= a2 + (2ab – 4ab) + b2
= a2 – 2ab + b2
= (a – b)2 = VT (đpcm)
+ Áp dụng, tính:
a) (a – b)2 = (a + b)2 – 4ab = 72 – 4.12 = 49 – 48 = 1
b) (a + b)2 = (a – b)2 + 4ab = 202 + 4.3 = 400 + 12 = 412.
\(\left(a+b\right)^2-4ab\)
\(=a^2+2ab+b^2-4ab\)
\(=a^2-2ab+b^2\)
\(=\left(a-b\right)^2=VT\left(đpcm\right)\)
\(1\ge a+b\ge2\sqrt{ab}\Rightarrow ab\le\dfrac{1}{4}\) \(\Rightarrow\dfrac{1}{ab}\ge4\)
Do đó:
\(ab+\dfrac{1}{a^2}+\dfrac{1}{b^2}\ge ab+\dfrac{2}{ab}=\left(ab+\dfrac{1}{16ab}\right)+\dfrac{31}{16}.\dfrac{1}{ab}\ge2\sqrt{\dfrac{ab}{16ab}}+\dfrac{31}{16}.4=\dfrac{33}{4}\)
Dấu "=" xảy ra khi \(a=b=\dfrac{1}{2}\)
