toán CASIO 8
cho đa thức P(x)=x6+ax5+cx4+bx3+dx2+ex+f có giá trị là 3;0;3;12;27 ;48 thì x lần lượt nhận các giá trị 1,2,3,4,5,6
Xác định hệ số a,b,c,d,e,f
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 4 2018
Có hàm số xác định trên cả R và f '(x) chỉ đổi dấu khi qua các điểm x=-1;x=1. Vậy hàm số có đúng hai điểm cực trị x=-1;x=1
Chọn đáp án A.
31 tháng 8 2017
Giải trên máy Casio fx-570MS ( Casio fx-570 tương tự)
Nhắc lại: Đa thức P(x) chia hết cho ax + b khi và chỉ khi P(-ba)=0
Dư của phép chia đa thức P(x) cho ax + b là P(-ba)
Quy trình bấm phím như sau:
1. Ghi vào màn hình: 6A3 -7A2 -16A
CM
4 tháng 3 2017
Chọn đáp án C.
Ta có
Đặt t = 1 - 2 x bất phương trình trở thành f ' t < t - 1
kẻ thêm đường thẳng y = x - 1 qua hai điểm (1;0);(3;2) trên đồ thị
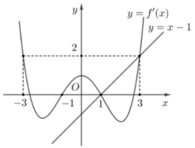
Ta có f ' t < t - 1
Đối chiếu các đáp án chọn C
28 tháng 7 2023
A(x)=F(x)-G(x)
=1+x+x^2+...+x^100-x^2-x^4-...-x^100
=1+x+x^3+...+x^99
Số số lẻ từ 1 đến 99 là (99-1):2+1=50(số)
A(-1)=1+(-1)+(-1)^3+...+(-1)^99
=1-50*1=1-50=-49