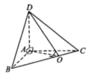
Cho tứ diện ABCD có B A C ^ = C A D ^ = D A B ^ = 90 0 , A B = 1 , A C = 2 , A D = 3 . Côsin của góc giữa hai mặt phẳng (ABC) và (BCD) là
![]()
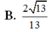
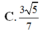
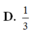
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Sửa đề: AD//BC
Ta có: AD\(\perp\)AB(gt)
BC\(\perp\)AB(gt)
Do đó: AD//BC(Định lí 1 từ vuông góc tới song song)
b) Ta có: AD//BC(cmt)
nên \(\widehat{D}+\widehat{C}=180^0\)(hai góc trong cùng phía)
\(\Leftrightarrow4\cdot\widehat{C}=180^0\)
hay \(\widehat{C}=45^0\)
Ta có: \(\widehat{D}=3\cdot\widehat{C}\)
nên \(\widehat{D}=135^0\)

a) Có AD ⊥ AB( góc A vuông)
BC ⊥ AB( góc B vuông)
=> AD // BC
b) Có tứ giác ABCD= 360 độ
mà A = B= 90 độ
=> C + D= ABCD - A - B
= 360 độ - 90 độ - 90 độ
= 180 độ
Có D = 3C và C + D = 180 độ
=> C = 45 độ
=> D = 135 độ
c) Có ABCD= 360 độ
A = B= 90 độ
=> C + D= 180 độ
=> D =180 độ - C
+) D - C = 30 độ
<=> 180 độ - C - C = 30 độ
<=> 2C= 150 độ
<=> C = 75 độ
=> D = 105 độ
Vậy a) AD // BC
b) C = 45 độ
D = 135 độ
c) C = 75 độ
D = 105 độ

\(S_{\Delta ACD}=\dfrac{1}{2}AC.AD.sin\widehat{CAD}=\dfrac{a^2\sqrt{3}}{4}\)
\(V=\dfrac{AB.AC.AD}{6}.\sqrt{1+2cos90^0.cos60^0.cos120^0-cos^290^0-cos^260^0-cos^2120^0}=\dfrac{a^3\sqrt{2}}{12}\)
\(\Rightarrow d\left(B;\left(ACD\right)\right)=\dfrac{3V}{S}=\dfrac{a\sqrt{6}}{3}\)

Chọn B
Mà ∠ B = ∠ A + 10 ° (2)
nên từ (1) và (2) => ∠ C - 10 ° = ∠ A + 10 ° => ∠ C = ∠ A + 20 °
Ta có: ∠ D = ∠ C + 10 ° => ∠ D = ∠ A + 20 ° + 10 ° => ∠ D = ∠ A + 30 °
Ta có : ∠ A+ ∠ B+ ∠ C+ ∠ D = 360 ° ( tổng bốn góc của tứ giác)
=> ∠ A+ ∠ A + 10 ° + ∠ A + 20 ° + ∠ A + 30 ° = 360 °
=> 4 ∠ A + 60 ° = 360 °
Do đó: ∠ A= 75 °
=> ∠ B = ∠ A + 75 ° + 10 ° = 85 °
=> ∠ C= ∠ A+ 20 ° = 95 °
=> ∠ D= ∠ A+ 30 ° = 105 °

a) C−D=20o
Mà ta có C+D=360o−(A+B)=360o−(60o+90o)=210o (tổng 4 góc trong một tứ giác bằng 360o)
⇔C−D+C+D=20o+210o
⇔2C=230o
⇒C=115o và D=95o
Góc ngoài của tứ giác tại đỉnh C là 180o−115o=65o
Xét tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)( tổng các góc trong tứ giác)
\(\Rightarrow\widehat{C}+\widehat{D}=360^0-\widehat{A}-\widehat{B}=360^0-60^0-90^0=210^0\)
Ta có: \(\left\{{}\begin{matrix}\widehat{C}+\widehat{D}=210^0\\\widehat{C}-\widehat{D}=20^0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{C}=\left(210^0+20^0\right):2=115^0\\\widehat{D}=\left(210^0-20^0\right):2=95^0\end{matrix}\right.\)

a: Xét tứ giác ABCD có
\(\widehat{A}+\widehat{C}=180^0\)
Do đó: ABCD là tứ giác nội tiếp

Xét tứ giác ABCD có \(\widehat{A}+\widehat{C}=180^0\)
nên ABCD là tứ giác nội tiếp

a) \(a^2+b^2+c^2+d^2=ab+bc+ac+cd.\)
<=>\(2a^2+2b^2+2c^2+2d^2=2ab+2ac+2bc+2cd\)
<=>\(2a^2+2b^2+2c^2+2d^2-2ab-2bc-2ac-2cd=0\)
<=>\(\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ac+a^2\right)+\left(d^2-2cd+c^2\right)\)=0
<=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2+\left(d-c\right)^2=0\)
=>a=b=c=d
=> ABCD là hình thoi