Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
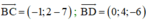
(BCD) nhận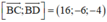 
là 1 vtpt
⇒ (BCD): 16x – 6y – 4z + 8 = 0
hay (BCD): 8x – 3y – 2z + 4 = 0.
Vecto pháp tuyến của mặt phẳng (ACD) vuông góc với hai vecto A C → = 0 ; - 1 ; 1 v à A D → = - 1 ; - 1 ; 3
Chọn C
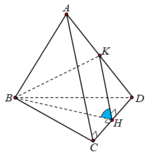
Gọi H là trung điểm cạnh CD và K là trung điểm cạnh AD.
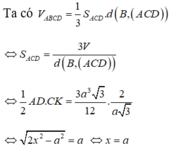
Tam giác ACD có CA=CD=x=a ; AD = a 2 => tam giác ACD vuông cân tại C
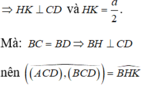
Mặt khác:
Tam giác ABD có:
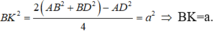
Tam giác BHK có:
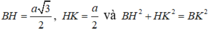
=> Tam giác BHK vuông tại H ⇒ B H K ^ = 90 o hay A C D , B C D ^ = 90 o
Gọi H là trung điểm BC
Vì \(\Delta BDC\) vuông tại D nên H là tâm đường tròn ngoại tiếp \(\Delta BDC\)
Vì \(\Delta ABC\) cân tại A nên AH vuông góc với BC
Mà (ABC) vuông góc (BDC) nên AH vuông góc với (BDC) tại H
\(\Rightarrow\) tâm mặt cầu ngoại tiếp tứ diện ABCD phải nằm trên đường thẳng AH
Chọn điểm O thuộc đường thẳng AH sao cho OA=OB thì O chính là tâm mặt cầu cần tìm
(bạn tự tính) được \(R=\frac{a^2}{b}\)
Gọi O là giao điểm của AC và BD. Dễ thấy \(\Delta OAB\) vuông tại O và \(OB=\dfrac{a\sqrt{3}}{2}\). Từ đó \(OA=\sqrt{AB^2-OB^2}=\sqrt{\left(\dfrac{\sqrt{3}}{2}a\right)^2-a^2}=\sqrt{\dfrac{1}{4}a^2}=\dfrac{a}{2}\) \(\Rightarrow AC=a\).
Vì \(SA\perp mp\left(ABCD\right)\) nên \(SA\perp AC\) tại A hay \(\Delta SAC\) vuông tại A.
Lại có \(\tan SAC=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\) nên \(\widehat{SAC}=60^o\), suy ra góc giữa SC và mp(ABCD) bằng 60o \(\Rightarrow\) Chọn A
Chỗ \(\widehat{SAC}\) em sửa lại là \(\widehat{SCA}\) mới đúng ạ.
Mặt phẳng ( α ) đi qua điểm D và song song với mặt phẳng (ABC) nên ( α ) cũng có vecto pháp tuyến là n ' → = (1; 1; 1)
Vậy phương trình của ( α ) là: (x – 4) + (y) + (z – 6) = 0 hay x + y + z – 10 = 0.
