Trong không gian, cho tam giác ABC đều cạnh a . Tính thể tích V của khối tròn xoay nhận được khi quay tam giác ABC xung quanh trục BC.
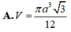
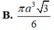
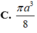
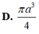
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn D
Tam giác ABC quay quanh trục là đường thẳng BC tạo ra hai khối nón:
-Khối nón đỉnh B, đường sinh BA.
-Khối nón đỉnh C, đường sinh CA.
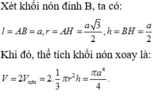

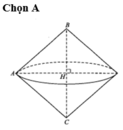
Tam giác ABC quay quanh trục là đường thẳng BC tạo ra hai hình nón.
-Hình nón đỉnh B, đường sinh BA.
-Hình nón đỉnh C, đường sinh CA.
Xét hình nón đỉnh B ta có:
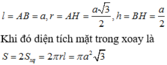

Chọn C.
Phương pháp:
Dựng hình, xác định các hình tròn xoay tạo thành khi quay và tính tỉ số thể tích.
Cách giải:
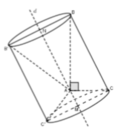
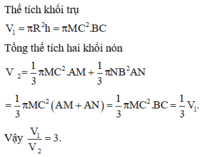

2:
\(\widehat{B'C;\left(A'B'C'\right)}=45^0\)
=>\(\widehat{\left(B'C;B'C'\right)}=45^0\)
=>\(\widehat{C'B'C}=45^0\)
Xét ΔCC'B' vuông tại C' có \(\widehat{C'B'C}=45^0\)
nên ΔCC'B' vuông cân tại C'
=>CC'=B'C'=a*căn 2
Thể tích khối lăng trụ là:
\(V=S_{BAC}\cdot CC'=a\sqrt{2}\cdot\dfrac{1}{2}a^2=\dfrac{\sqrt{2}}{2}\cdot a^3\)