Tập xác định của hàm số: y = cot x là:
A. D = ℝ \ k π 2 | k ∈ ℤ .
B. D = ℝ \ kπ | k ∈ ℤ .
C. D = ℝ \ π 4 + kπ | k ∈ ℤ .
D. D = ℝ \ π 2 + kπ | k ∈ ℤ .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Hàm số y = sin 2x thỏa mãn tính chất trên, các hàm số y = tan x, y = cot x cần điều kiện của x.

Đáp án B
TXĐ của hàm y = tanx là D = ℝ \ π 2 + k π | k ∈ ℤ nên TXĐ của hàm y = tan 2 x là D = ℝ \ π 4 + k π 2 | k ∈ ℤ
TXĐ của hàm y = cot x là D = ℝ \ k π | k ∈ ℤ nên TXĐ của hàm y = cot 2 x là D = ℝ \ k π 2 | k ∈ ℤ

a) + Hàm số y = cos x có chu kì 2π.
Do đó: cos 2.(x + kπ) = cos (2x + k2π) = cos 2x.
⇒ Hàm số y = cos 2x cũng tuần hoàn với chu kì π.
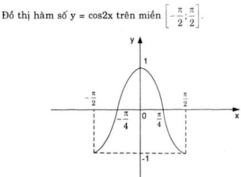
Từ đó suy ra
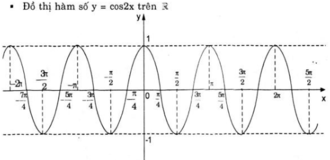
b. y = f(x) = cos 2x
⇒ y’ = f’(x) = (cos 2x)’ = -(2x)’.sin 2x = -2.sin 2x.
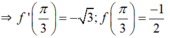
⇒ Phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π/3 là:
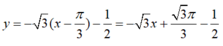
c. Ta có: 1 – cos 2x = 2.sin2x ≥ 0.
Và 1 + cos22x > 0; ∀ x
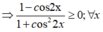
⇒ 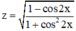 luôn xác định với mọi x ∈ R.
luôn xác định với mọi x ∈ R.

Chọn C
Hàm số
y
=
log
2
(
4
x
-
2
x
+
m
)
có tập xác định là D =
ℝ
![]()
Đặt ![]() Khi đó, bất phương trình (1) trở thành:
Khi đó, bất phương trình (1) trở thành:
![]()
![]()
Xét hàm số ![]()
Ta có: f'(t) = 2t + 1; f'(t) = 0 ⇔ t = 1 2
Bảng biến thiên:
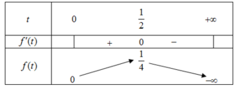
Dựa vào bảng biến thiên, suy ra 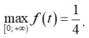
Từ (*) suy ra 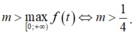

Đáp án D
Hàm số có tập xác định D = ℝ
⇔ x 2 − 2 m x + 4 > 0 , ∀ x ∈ ℝ
⇔ Δ ' < 0 ⇔ m 2 − 4 < 0 ⇔ − 2 < m < 2

Đáp án D
Tại -1 hàm số không xác định nên không nghịch biến trên ( - ∞ ; 3 )

Đáp án D
Khẳng định sai là “Hàm số nghịch biến trên khoảng − ∞ ; 1 ” do hàm số không xác định tại x = - 2
Đáp án B